La constante de Planck

José L. Ocaña
E.T.S. de Ingenieros Industriales (UPM)

Resumen

El 20 de mayo de 2019 entró en vigor una nueva definición de las unidades del Sistema Internacional que suponía una verdadera revolución con relación a las definiciones anteriores, al incorporar de forma explícita su dependencia de varias constantes universales y eliminando por completo su definición con referencia a patrones materiales (como era el caso del kilogramo patrón). Esta nueva definición se realiza en base a la consideración con carácter exacto (sin incertidumbre asociada) de siete constantes físicas fundamentales, entre ellas la constante de Planck, objeto del presente artículo. En los distintos epígrafes en que se ha dividido el mismo, se recordará, en primer lugar, el origen histórico de la introducción por Max Planck de dicha constante en su formulación de la distribución de energía en la radiación del Cuerpo Negro, para pasar, a continuación, a un análisis de la significación de la constante en todo el desarrollo posterior de la Física Cuántica hasta nuestros días y a un análisis de su carácter fundamental con vistas a su consideración como constante con valor exacto en la nueva definición de la unidad de masa.

Abstract

On May 20, 2019, a new definition of the units of the International System came into force, which represented a true revolution in relation to the previous definitions, by explicitly incorporating their dependence on several universal constants and completely eliminating their definition with reference to material standards (as was the case with the standard of kilogram). This new definition is made based on the exact consideration (without associated uncertainty) of seven fundamental physical constants, among them the Planck constant, which is the subject of this article. In the different sections into which it has been divided, it will be recalled, first, the historical origin of the introduction by Max Planck of said constant in his formulation of the energy distribution in the radiation of the Black Body, followed by an analysis of the significance of the constant throughout the subsequent development of Quantum Physics till the present day and an analysis of its fundamental character in order to considering it as a constant with exact value in the new definition of the unit of mass.

1. INTRODUCCIÓN

La constante de Planck es una constante física que desempeña un papel fundamental en el desarrollo de la Física Cuántica y debe su nombre al científico alemán Max Planck, que la utilizó por primera vez en la formulación de la distribución energética de la radiación emitida por los cuerpos a elevada temperatura (radiación del “Cuerpo Negro”).

El origen de la Teoría Cuántica y el trabajo teórico de Max Planck son, sin duda, de los episodios más citados y analizados a lo largo del desarrollo de dicha disciplina, dado que constituyen el punto de partida de dicho desarrollo. Aunque el propio Planck, en su carta a Robert Wood[1], parecía reconocer abiertamente que la introducción del “cuanto de energía”, hν, había respondido a un “acto de desesperación” admitiendo la propiedad del tratamiento termodinámico estadístico desarrollado por Boltzmann, estudios más detallados sobre sus progresos y su críptica descripción de dichos avances (mirados especialmente a través de las notas al pie de sus escritos) parecen apuntar que el trabajo de Planck sí tuvo una apreciable coherencia interna y se enraíza fuertemente en su convicción de que la progresión del conocimiento debía fundarse inevitablemente en la existencia de “Constantes Universales” que proporcionaran un verdadero significado físico a las teorías y sus experimentos de confirmación.

Tal punto de vista ya había sido puesto en práctica por C.F. Gauss con la proposición del Sistema de Unidades que lleva su nombre y expresado por J.C. Maxwell al disertar en relación con la constitución molecular de la materia[2]: “Si queremos obtener patrones de longitud, tiempo y masa que sean absolutamente permanentes, debemos buscarlos no en las dimensiones, el movimiento y la masa de nuestro planeta, sino en la longitud de onda, el período de vibración y la masa absoluta de (…) imperecederas e inalterables y perfectamente semejantes moléculas”.

Planck, en su célebre cita de 1900 en relación con la necesidad de consideración de constantes físicas fundamentales al objeto de una adecuada descripción de los fenómenos físicos[3] ya advirtió: “Con la ayuda de constantes fundamentales… tenemos la posibilidad de establecer unidades de longitud, tiempo, masa y temperatura que retengan necesariamente su significado para todas las culturas, incluso las extraterrestres y no humanas” y en uno de sus primeros artículos de alcance divulgativo tras la plena interpretación de su descubrimiento de la ley de emisión del “Cuerpo Negro”[4], constató: “…la Física Teórica muestra una marcada tendencia hacia un sistema unitario, liberándose de elementos antropomórficos…”.

En opinión de muchos de los estudiosos que han analizado el trabajo de Planck y, en particular, su camino hacia su descubrimiento fundamental[6], el origen de la búsqueda por su parte de “constantes universales” era su convicción personal sobre el carácter absoluto de las leyes físicas y de que sólo dichas constantes eran capaces de proporcionar teorías con un “significado físico real”[7]. En dicho camino, el trabajo de Planck tomó la forma de un programa de investigación que culminó en diciembre de 1900 con la proposición de su renombrada ley y, aunque transcurrió por una trayectoria a veces tortuosa, mantuvo su propósito original de búsqueda de un significado absoluto de las leyes termodinámicas, y en especial, del significado físico de la entropía, de manera que la solución finalmente propuesta para la ley de distribución de energías en el espectro de emisión del “Cuerpo Negro” sólo le resultó satisfactoria en la medida en que parecía implicar (y de hecho implicaba) una relación de coherencia entre magnitudes físicas con intervención de “constantes naturales absolutas” independientes de lugar, tiempo u otras consideraciones[8].

A lo largo del presente artículo se retornará, una vez analizadas la génesis histórica de la constante h en el contexto de la emergente Teoría Cuántica durante el primer tercio del siglo XX y su significación en las áreas clave de la Física de nuestros días, a este punto de vista de formulación de las teorías clave en la descripción de la Naturaleza en función de “constantes física universales”, intentando enlazar con el espíritu que ha guiado la reciente reformulación del Sistema Internacional de Unidades sobre la base de dicho tipo de constantes.

2. EL HALLAZGO CLAVE DE PLANCK Y LA INTRODUCCIÓN DE SU CONSTANTE UNIVERSAL

La historia del proceso científico que llevo a Planck a la proposición de su célebre “ley de distribución de energías en el espectro normal” había comenzado a finales de 1894, momento en el que comenzó a establecer vínculos novedosos entre tres de las líneas de investigación científica en curso por aquella época, a saber, el electromagnetismo, la termodinámica y el estudio de la estructura de la materia, en particular la teoría cinético-molecular de los gases. En la práctica, el tema de investigación que condujo a Planck a su formulación basada en la admisión de un carácter discreto para la distribución de la energía emitida por los cuerpos radiantes fue el estudio de este tipo de radiación iniciado por G. Kirchhoff[9]. Dicho proceso fue intenso y no exento de dificultades y puede ser consultado en muchas de las excelentes revisiones históricas y de análisis científico realizadas sobre el mismo[10].

El hecho fundamental es que el 14 de diciembre de 1900, en su presentación ante la Real Academia Prusiana de Ciencias[11], y sobre la base de los recientes ajustes realizados sobre los datos experimentales de Lummer y Pringsheim[2], presentó una ley de distribución espectral de la radiación emitida por los cuerpos a elevada temperatura (“Cuerpos Negros”), que, si bien constituía formalmente un mero ajuste experimental sin explicación aparente, era capaz de dar por primera vez cumplida cuenta de todos los hallazgos experimentales conocidos, superando los obtenidos varios años atrás por W. Wien en la región infrarroja del espectro y siendo, además, apropiado para la región de elevadas frecuencias (a partir de la región ultravioleta), en la que la ley de distribución teórica de Rayleigh y Jeans fracasaría dando lugar al problema de la “catástrofe ultravioleta”[13].

La distribución propuesta por Planck, que además predecía perfectamente la ley experimental del desplazamiento de Wien[14] y la ley de emisión de Stefan-Boltzmann[15], establecía para la densidad espectral de energía de las ondas electromagnéticas emitidas por un cuerpo a una determinada temperatura, T, la expresión:

Dicha expresión (que fue la inicialmente propuesta por Planck) llevaba ya el germen de lo que habría de ser el hecho fundamental de la distribución discreta en paquetes finitos de la energía total radiada por el cuerpo en términos de la constante h.

En efecto, a través de la adopción del punto de vista estadístico en la descripción de las variables termodinámicas (específicamente la entropía) de acuerdo con lo propuesto por L. Boltzmann[16] y la consideración del equilibrio termodinámico como el estado de máxima entropía de acuerdo con la en aquel entonces reciente teoría de R. Clausius[17], Planck introdujo por primera vez la necesidad de distribución de la energía del sistema en elementos discretos como forma de que las expresiones combinadas del número de ondas emitidas y la energía total del sistema condujeran a una expresión de la entropía acorde a los resultados estrictamente termodinámicos conocidos hasta el momento.

En palabras del propio Planck: “Debemos considerar ahora la distribución de energía entre cada tipo de resonador, en primer lugar la distribución de la energía E entre los N resonadores de frecuencia n. Si consideramos a E infinitamente divisible, entonces son posibles un número infinito de distribuciones diferentes. Nosotros, sin embargo, suponemos –y ese es el punto esencial- que E está compuesta de un número determinado de partes finitas iguales y empleamos en su denominación la constante natural \(h=6,55\:\: 10^{-27}\) (ergios por segundo). Esta constante, multiplicada por la frecuencia n del resonador, da el elemento de energía e en ergios, y dividiendo E por e obtenemos el número P de elementos de energía a distribuir entre los N resonadores”.

La primera derivación de Planck, tal como fue publicada, omitía algunos pasos esenciales como, en particular, la incorporación de la relación de Boltzmann entre entropía y probabilidad y, por ello, hasta la aparición en 1906 de sus “Lecciones sobre la Teoría de la Radiación Térmica”[18], los investigadores coetáneos no llegaron a una interpretación correcta de su hipótesis. En 1906 (1909), H.A. Lorentz[19] derivó la ley de Planck en una forma semejante a la derivación de Boltzmann de la ley de distribución para los gases[20] . Desde entonces, pasando por la segunda edición de las “Lecciones” de Planck[21], publicada en 1913, dicha versión es la más conocida y utilizada. De acuerdo con estas versiones, e incorporando ya la nueva y recién definida constante h, la expresión final de la densidad espectral de energía de los modos de vibración del “Cuerpo Negro” en condiciones de equilibrio térmico a la temperatura T quedó expuesta en la forma:

expresión en la que las constantes a y b, identificadas por Planck como “constantes universales”, resultaban tener los valores:

En el citado Discurso de Aceptación del Premio Nobel, Planck confería un valor decisivo a la existencia de esta constante y reconocía textualmente “Esta constante suele denominarse Constante de Boltzmann, aunque, hasta donde yo sé, el propio Boltzmann nunca la mencionó….y nunca consideró la posibilidad de llevar a cabo una medición precisa de la misma”[22].

Según lo indicado, con el establecimiento de su ley de distribución de energía, Planck había llegado a encontrar algo más importante y fundamental que una simple derivación de su ley de distribución: había logrado un nexo cuantitativo y concreto entre la Teoría Electromagnética, la Termodinámica y la descripción microscópica de las propiedades de las partículas formulada a través de la emergente Mecánica Estadística desarrollada por Boltzmann. Su descubrimiento motivó de forma efectiva un giro fundamental en la evolución de la Física, toda vez que, durante los diez años que siguieron al mismo, las pruebas experimentales (cada vez más exigentes) no dejaron de confirmarla, requiriéndose, en consecuencia, una reconstrucción fundamental de las teorías establecidas.

La razón aparente por la que Planck llegó a la hipótesis de que la energía total del sistema radiante había de subdividirse de una manera discreta fue, la necesidad de establecer una correspondencia entre la distribución obtenida con lo exigido por la descripción probabilística de la entropía del sistema y su maximización en los estados de equilibrio como había mostrado Boltzmann. Sin embargo, entendida con propiedad, para poder representar realmente la distribución de equilibrio de la densidad de energía del “Cuerpo Negro”, la teoría de Planck no sólo requería esta hipótesis, sino que requería una hipótesis adicional (no formulada explícitamente por su autor) de que cada oscilador de la cavidad radiante no sólo debería tener energía discretamente cuantizada, sino que debería poder absorber y emitir energía en paquetes múltiplo de la cantidad hn, denominada por Planck elemento de energía.

Esta hipótesis fue formulada explícitamente de manera independiente por P. Ehrenfest[23] y A. Einstein[24], quienes, de esta forma, resultaron ser los verdaderos fundadores de la Teoría Cuántica de la radiación en la forma en que hoy la conocemos. Siguiendo el razonamiento de Planck, Ehrenfest y Einstein llegaron a la conclusión de que, al objeto de poder ser tratadas mediante el procedimiento estadístico construido por Planck sobre la teoría de Boltzmann, las ondas electromagnéticas emitidas por el cuerpo radiante deberían tener una naturaleza discontinua en energía. Como consecuencia de esta hipótesis adicional, Einstein logró en 1905 explicar de forma satisfactoria el efecto fotoeléctrico, hito fundamental para el desarrollo de la Teoría Cuántica que, en la práctica, valió tanto a Planck como a Einstein el Premio Nobel de Física (Ediciones de 1918 y 1921, respectivamente.

3. IMPACTO Y SIGNIFICACIÓN DE LA INCORPORACIÓN DE LA TEORÍA CUÁNTICA EN EL CONTEXTO DE LA FÍSICA DEL SIGLO XX

A partir de los hallazgos de Planck y Einstein, la Teoría Cuántica demostró de forma definitiva su valor en la por entonces muy activa investigación en curso sobre la estructura atómica. Así, en 1913, el físico danés N. Bohr aplicó dicha teoría a la elucidación de la estructura atómica mediante la formulación de sus célebres postulados[25]. De forma directa, Bohr postuló que en el seno de un átomo, un electrón sólo podía emitir o absorber energía en cantidades fijas y discretas, es decir, cuantizadas, con valores acordes a los predichos por Planck. Pero, así mismo postuló (de manera mucho más arriesgada) que, en su movimiento orbital alrededor del núcleo atómico, los electrones sólo podían seguir determinadas órbitas con un momento cinético orbital asimismo cuantizado, con valores múltiplos del “cuanto de acción”[26] de Planck (h) dividido por la constante 2π. Gracias al desarrollo del modelo atómico de Bohr los físicos de la época lograron comprender la razón de que cada elemento químico conocido radiaba y absorbía radiación electromagnética sólo de ciertas longitudes de onda, explicando de paso la ley experimental de Kirchhoff, base de todo el desarrollo realizado por Planck.

De la misma forma, y sobre la base de la explicación del efecto fotoeléctrico proporcionada por Einstein, A.H. Compton demostró a través de una serie de experimentos realizados entre 1919 y 1923[27] que cuando los rayos X colisionaban con electrones libres, los correspondientes cuantos de radiación asociados no sólo perdían una cantidad de energía correspondiente al cambio observado en su longitud de onda, sino que, a todos los efectos, sus colisiones con los electrones seguían enteramente las leyes de la mecánica (relativista) transfiriendo a estos parte de su cantidad de movimiento y actuando, por tanto, como verdaderas partículas a las que se podía atribuir una energía E=hυ, pero también una cantidad de movimiento p=hυ/c. De esta forma (pero no la única), volvió a quedar claro el papel fundamental que la cuantización de la energía y la acción mecánica (y con ello la constante de Planck) jugaban a nivel de la descripción de los fenómenos microscópicos. En la práctica, los resultados de Compton constituyeron, sin duda, una relación de la máxima importancia a la hora de relacionar las propiedades espectrales (electromagnéticas) de los cuantos de radiación (fotones) con sus propiedades mecánicas, un punto de referencia esencial para el establecimiento por de Broglie del principio de dualidad onda-corpúsculo, que resultó la verdadera piedra angular del desarrollo de la Teoría Cuántica basada en la descripción del movimiento de partículas a través de funciones de onda.

En efecto, el hecho de que la radiación electromagnética poseyera algunas propiedades similares a las partículas materiales (energía, cantidad de movimiento) indujo en 1924 a L. de Broglie a construir una teoría en la que postulaba la dualidad onda/corpúsculo para los cuantos de radiación (fotones) en cualquier experimento en el que se debieran poner de manifiesto sus propiedades “mecánicas”. En un artículo titulado “A Tentative Theory of Light Quanta”[28], de Broglie desarrolló las consecuencias de la combinación de la ecuación de Planck y Einstein para la energía de los fotones (E=hυ) con la expresión generalizada de la equivalencia masa-energía en el marco de la Teoría de la Relatividad Especial (o Restringida), formulada por Einstein en 1905[29] (E=mc²). A partir de este análisis especuló con la idea de que dicha equivalencia podía aplicarse a todas las partículas, en cuyo caso el comportamiento ondulatorio sería una propiedad universal de todos los objetos en movimiento. La hipótesis se formulaba sin ninguna evidencia experimental y parecía postularse en contra de todas las descripciones mantenidas clásicamente, pero resultó ser cierta y pudo ser verificada en las condiciones apropiadas.

El resultado fundamental de la hipótesis de de Broglie fue que cualquier partícula con una cantidad de movimiento, p, debería tener asociada como onda una longitud de onda de valor λ=h/p, resultado que se había podido inducir fácilmente a partir de la consideración del caso particular del fotón, para el cual, según la Teoría de la Relatividad Especial, era p=E/c. Con ello quedaba abierta de manera definitiva la vía para la consideración de las partículas en una dimensión ondulatoria, preludio de la formulación por parte de E. Schrödinger de su teoría del movimiento de las partículas a través de funciones de onda.

En efecto, en 1925, E. Schrödinger, utilizando analogías formales entre la Óptica y la Mecánica Clásica, postuló la forma de una ecuación de onda aplicable a la descripción del movimiento de partículas a través del hallazgo de la correspondiente solución en un entorno físico determinado caracterizado por su función potencial. La formulación de dicha Ecuación de Onda incorporaba la atribución a la partícula en movimiento de las propiedades ondulatorias postuladas por de Broglie, de manera que, asumiendo velocidades de movimiento muy inferiores a la de propagación de ondas electromagnéticas en el vacío (límite clásico), el movimiento de una partícula de masa m se podía considerar determinado a través de la solución, ψ(r,t), de la famosa ecuación de onda de Schrödinger:

formulada inicialmente por su autor en su forma unidimensional[30], y en la cual la constante ħ=h/2π  juega un papel fundamental.

La formulación de la ecuación de Schrödinger, con su descripción del movimiento de las partículas en términos de la función de onda \(\varPsi(\mathit{\boldsymbol{r}},t)\) (cuyas soluciones vienen limitadas por determinadas condiciones de compatibilidad derivadas de la forma funcional del potencial \(V(\mathit{\boldsymbol{r}})\) y cuyo significado físico viene asociado a la probabilidad de encontrar a la partícula en movimiento en unas coordenadas espacio-temporales concretas, \(P(\mathit{\boldsymbol{r}},t)=\left | \varPsi(\mathit{\boldsymbol{r}},t) \right |^{2}\) ), estableció de forma definitiva la forma de aproximación y el marco de descripción de los fenómenos físicos gracias a los cuales se han podido materializar decisivos desarrollos y descubrimientos a lo largo de la parte restante del siglo XX y hasta nuestros días.

En efecto, la Física Cuántica se ha revelado como la herramienta necesaria para la comprensión y predicción de toda clase de fenómenos físicos y está en la base de los avances tecnológicos de mayor relevancia a lo largo de todo el siglo XX y hasta la actualidad. A través de la elucidación de estructuras atómicas, moleculares y de materias en fase condensada, la Física Cuántica es la base de la Química moderna y de la Física del Estado Sólido, capaz de explicar satisfactoriamente el comportamiento de la materia y base para el desarrollo de la tecnología de semiconductores (de las cuales, el transistor de unión fue en su día el hito fundamental), de importancia esencial en nuestras vidas.

De la misma forma, desarrollos clave como la Tecnología Láser, la de superconductores y el desarrollo de todo tipo de herramientas de manipulación y caracterización de materiales (incluidas distintas técnicas de importancia fundamental para la Metrología) han motivado que, en el momento presente, los caminos de vanguardia de la ciencia y la tecnología sean prácticamente indistinguibles y se esté asistiendo a desarrollos sin precedentes en el campo del desarrollo de nuevos materiales. Y, en la perspectiva futura más inmediata, el desarrollo de las tecnologías basadas en la transmisión cuántica de información, base de los avances registrados en criptografía y computación cuánticas, ha permitido alcanzar hitos difícilmente imaginables en el momento de la formulación de la teoría de emisión del “Cuerpo Negro”.

4. LA CONSTANTE DE PLANCK COMO CONSTANTE PARADIGMÁTICA EN EL MARCO DE LA FORMULACIÓN DE TEORÍAS FÍSICAS BASADAS EN CONSTANTES UNIVERSALES

Según lo comentado en el epígrafe de Introducción, la tendencia hacia la completa eliminación de todas las características ligadas a la percepción humana de los conceptos físicos integrantes de las leyes de la Naturaleza constituyó una actitud recurrente en todo el desarrollo de la carrera científica de Planck, así como una base firme para su filosofía del conocimiento científico en general. En su citada contribución, “La unidad de la concepción física del Universo” [31], Planck criticaba el punto de vista de algunos científicos de su época (especialmente E. Mach) caracterizada por la imposición de una imagen física del Universo demasiado marcada por las apreciaciones ligadas a los sentidos humanos, especialmente en lo que se refería a unidades de medida.

En 1899, en su contribución a la Sociedad Física Alemana, el 18 de mayo, titulado “Sobre los Procesos Irreversibles de la Radiación”[32], en el que dio su primera derivación (aún inexacta) de su teoría del “Cuerpo Negro”,propuso por primera vez un sistema de unidades basado únicamente en las constantes universales contenidas en su ley de radiación, la constante gravitatoria, G, y la velocidad de la luz en el vacío, c. Aparte de las consideraciones de J.C. Maxwell también citadas en la Introducción, un punto de vista semejante había sido ya expuesto por G.J. Stoney[33] y P. Drude[34] antes que Planck.

En efecto, en un artículo con el significativo título “Sobre las unidades físicas de la Naturaleza”, Stoney propuso la necesidad de identificar un nuevo sistema de unidades de medida que considerara la Naturaleza en su verdadera esencia, de manera que, en su consideración, sería necesaria la identificación de tres “constantes universales” a partir de las cuales pudieran ser derivadas las unidades de longitud, masa y tiempo. De la misma forma, P. Drude expresó en 1897 su esperanza en la creación de un sistema de unidades de medida basado exclusivamente en las propiedades del éter. Aunque no parece haber relación directa entre las consideraciones de Stoney, Drude y Planck, sí es posible encontrar una línea de pensamiento común entre sus contribuciones, a saber, una necesidad de liberación de los desarrollos científicos de cualquier aspecto subjetivo que pudiera limitarlos.

En su citada contribución, Planck propuso, apartándose de la senda marcada previamente por Wien, la dependencia de la entropía de los resonadores emisores de energía radiante en términos de las dos constantes a y b, según lo expuesto en párrafos precedentes, y concluía con las palabras: “Sería perfectamente imaginable que todos los sistemas de unidades de medida adoptados hasta el momento perdieran total o parcialmente su significación natural original”.

Para remediar esta situación, Planck propuso la creación de un nuevo sistema de unidades de medida basado en magnitudes supuestamente independientes de cualquier contingencia. En concreto, refiriéndose a las nuevas constantes halladas, escribió su célebre cita: “Las constantes a y b proporcionan (junto con las constantes c y G) la posibilidad de identificar las nuevas unidades de longitud, masa, tiempo y temperatura que, con independencia de cuerpos específicos o circunstancias particulares, necesariamente mantengan su significado en cualquier época…, pudiendo ser, por tanto, consideradas como “unidades naturales de medida”.

En efecto, operando dimensionalmente las referidas “constantes universales”, Planck llegó a la definición de las unidades de medida del sistema propuesto (expresadas aquí en unidades del Sistema Internacional):

sentenciando finalmente: “Estas magnitudes retendrán su significado natural en la medida en que las leyes de la Gravedad, la propagación de la luz en el vacío y los dos principios de la teoría del calor se mantengan y, aunque sean medidas por diferentes inteligencias y utilizando diferentes métodos, deben permanecer siempre inalterables”.

Hay que recordar que la relación obtenida por Planck entre las constantes a y b de su particular sistema de unidades fue inicialmente obtenida a través de argumentos termodinámicos clásicos referidos a la relación entre la entropía y la energía interna de los resonadores emisores de radiación que finalmente desembocaron en el ajuste de los datos experimentales de Lutter y Pringsheim, hecho que, a su vez, condujo a la proposición de la forma funcional del espectro de emisión del “Cuerpo Negro”. Sin embargo, dicha expresión escondía una relación mucho más profunda una vez que se considera la descripción termodinámica de la entropía en términos de la probabilidad debida a Boltzmann. Dicha relación, escrita en términos de otras dos constantes tenidas como fundamentales en la época de formulación de la ley de Planck, a saber, la constante R de los gases y el número de Avogadro, resulta ser:

A través de esta ligazón (por la que Planck reconocía explícitamente el trabajo de Boltzmann), quedó introducido el avance verdaderamente revolucionario de la definición de la entropía (y, por ende, el resto de magnitudes térmicas) en términos estrictamente absolutos y no ligados a técnicas experimentales humanamente condicionadas, confiriendo así su verdadera significación a los principios establecidos de la Termodinámica.

Una vez reconocidas como constantes fundamentales las propias constantes de Boltzmann y Planck (en lugar de las inicialmente consideradas a y b) además de las consabidas c y G, el “Sistema de Unidades Naturales de Medida” finalmente propuesto por Planck fue el basado en las magnitudes fundamentales (presentado aquí con valores numéricos actualizados en el SI):

a las que habría que añadir, por completitud, y al objeto de cubrir los fenómenos electromagnéticos, la unidad de carga eléctrica:

donde \(k_{e}= \frac{1}{4\pi \varepsilon_{0}} \equiv\) Constante de fuerza electrostática

Este sistema fue mantenido por Planck en todas las ediciones posteriores de sus Lecciones y, tras un cierto período durante el cual no fue considerado como de utilidad en función de lo apartado de los valores de sus unidades definitorias en términos de los valores usuales de dichas magnitudes ligados a la actividad humana (mejor representados en la práctica por el metro, el kilogramo y el segundo), fue nuevamente tomado en consideración a partir de los años 30 del pasado siglo en relación con los desarrollos en curso sobre la teoría general de la Relatividad, la Cosmología y la Física Cuántica, para las cuales resultó de utilidad la definición de los parámetros:

en los cuales la constante original de Planck, h, ha dejado paso, en función de su más adecuada dimensionalidad como cuanto de acción[36], a su expresión en términos referidos a frecuencias angulares (y, por tanto, a unidades angulares naturales), ħ=h/2π. Combinando estas ecuaciones se obtiene, por ejemplo:

A pesar de que, por las razones expuestas, el sistema de unidades de Planck no constituye un sistema de unidades de gran utilidad práctica, el hecho de su definición a través de constantes fundamentales de la Naturaleza y su inclusión de constantes físicas de tanta significación como h, k, c y G permite, sin embargo, reflexionar sobre la conveniencia de que cualquier sistema de unidades científicamente fundado y, por tanto, con una estimable estabilidad a largo plazo, esté definido sobre la base de verdaderas “constantes físicas naturales”, tal y como parece ser el espíritu de la nueva definición, recién entrada en vigor, del Sistema Internacional de Unidades, que aparece en la Introducción de su presentación[37].

Ese ha sido el intento de algunas otras propuestas de sistemas “naturales” de unidades, habiéndose de reconocer, no obstante, las dificultades existentes para su implantación más allá del marco físico estricto para el que se han definido, precisamente como consecuencia de la general prevalencia del desarrollo del Sistema Internacional en sus sucesivas ediciones, las cuales, independientemente de la fundamentación física profunda de sus unidades, ha constituido y constituye un marco estable para el desarrollo científico-tecnológico cuya vigencia merece ser preservada.

5. PRESENCIA DE LA CONSTANTE DE PLANCK EN ÁMBITOS CIENTÍFICO-TECNOLÓGICOS CLAVE Y SU IMPLICACIÓN EN LA DEFINICIÓN DE NUEVOS PATRONES DE MEDIDA

La constante de Planck es una constante física fundamental que, a través de su marco natural de existencia, la Física Cuántica, impregna toda la ciencia y tecnología de nuestros días, existiendo multitud de fenómenos físicos, químicos y biológicos en cuyas leyes interviene y a partir de los cuales puede ser determinada experimentalmente.

En su excelente artículo sobre la naturaleza conceptual de las constantes físicas, Jean-Marck Lévy-Leblond, uno de los más prestigiados profesores en el ámbito de la enseñanza de la Física Cuántica, señala como el papel de una constante universal, en la medida que constituye la base para la formulación de nuevos conceptos, decrece normalmente en importancia a medida que transcurre el tiempo y la novedad de dichos conceptos se difumina[38]. Sin embargo, no se considera que este sea el caso de la constante h.

Las primeras mediciones de esta constante se efectuaron a partir del efecto Fotoeléctrico. Una de las primeras determinaciones experimentales directas de h (y, congruentemente, de la constante de Stefan-Boltzmann, σ) se debe a R. Millikan[39], quien planteó la misma sobre la base de la linealidad de la relación entre el potencial de interrupción del efecto fotoeléctrico y la frecuencia de la radiación aplicada.

Con posterioridad, un importante número de determinaciones sistemáticas han venido siendo realizadas en conexión con determinadas verificaciones en el marco de la Física Atómica, Molecular, del Estado Sólido y Nuclear, siendo significativas por su valor conceptual las realizadas en conexión con la determinación de la Constante de Estructura Fina (\(\alpha = \frac{e^{2}}{(4\pi \varepsilon_{0}\hbar c)}\)), pieza clave en el ámbito de la Electrodinámica Cuántica[40] y las asociadas a la determinación experimental del Magnetón de Bohr (\(\mu_{B}=\frac{e\hbar}{2m_{e}}\)), a su vez clave en el desarrollo de la Espectroscopía de Resonancia Magnética)[41].

A nivel de laboratorio docente, existen multitud de aproximaciones que permiten obtener valores razonablemente precisos de la constante[42], pero es, sin duda, a través de su implicación en fenómenos físicos de gran significación científico-tecnológica como se puede vislumbrar su verdadero nivel de relevancia en el marco del conocimiento de nuestros días.

Tal es el caso de la intervención de la Física Cuántica (y, por tanto, de su magnitud señera, la Constante de Planck) en dos fenómenos físicos de gran relevancia (ambos merecedores de sendos premios Nobel para sus descubridores) cuales son el Efecto Josephson[43] (establecimiento de corriente electrónica por efecto túnel en superconductores) y la observación del carácter cuantizado de la resistencia de Efecto Hall en estructuras electrónicas bidimensionales[44] , efectos que, además, han proporcionado un importante avance hacia la medida de la Constante de Planck con los niveles más bajos de incertidumbre conocidos hasta el momento y han propiciado su utilización como constante “fija” (con incertidumbre nula) en la última redefinición de las unidades del Sistema Internacional[45].

En efecto, en 1962, B. Josephson, estableció las ecuaciones para la intensidad de corriente y diferencia de potencial aplicables a una unión de dos superconductores separados por una barrera aisslante, las cuales predecían que, polarizada la unión con una tensión V (y en ausencia de otra excitación externa), el sistema actuaba como un oscilador de frecuencia \(f_{J}=\frac{2e}{h}V\) a causa del efecto túnel (de naturaleza típicamente cuántica) de portadores de Cooper[46] a través de la barrera aislante y que, a la inversa, el atrapamiento de portadores con arreglo a frecuencias fijas (que podían generarse mediante la irradiación de la unión por haces de microondas), podían encontrarse sucesivos niveles escalonados de diferencia de potencial a través de la unión (de valores múltiplos de la frecuencia de excitación, es decir, \(V_{n}=n\frac{h}{2e}f=\frac{nf}{^{K_{J}}}\)), lo cual constituía un procedimiento notable de discretización de niveles de tensión (macroscópica) en función de múltiplos enteros directamente dependientes de constantes físicas fundamentales.

Dado que la precisión con la que pueden determinarse experimentalmente las frecuencias de excitación es elevada, el procedimiento lleva claramente a la posibilidad de correlación de las mismas con diferencias muy finas de diferencias de potencial supuestos conocidos con gran precisión los valores de las constantes fundamentales intervinientes, o, a la inversa, la determinación de las mismas con gran precisión en la medida en que sean directamente apreciables con gran precisión valores de diferencia de potencial(47).

De la misma forma, tratando de diseñar un nuevo método de determinación precisa de la constante de estructura fina, α, K. von Klitzing y colaboradores encontraron que la medida de la conductividad transversal de efecto Hall transversal de gases de electrones correspondientes a configuraciones bidimensionales (obtenibles en dispositivos MOSFET) proporcionaba, en determinadas condiciones de densidad de portadores y campo de inducción magnética aplicado, valores fijos definidos, independientes de la geometría del dispositivo y espaciados, a medida que se hacía crecer dicho campo, un número entero de veces el valor de una constante característica de valor \(\frac{h^{2}}{e}\) (es decir, \(\sigma_{H} = \frac{1}{R_{H}} = \frac{n}{R_{K}} = n\frac{h^{2}}{e}\))(48). Dicho comportamiento ligaba asimismo valores macroscópicos determinables por vía experimental, como la resistividad del gas de electrones, con los valores de constantes físicas fundamentales (de nuevo la carga del electrón y la Constante de Planck), quedando igualmente expedita la vía, bien para la determinación precisa de los valores de resistividad sobre la base de constantes físicas supuestas como conocidas o bien, de forma inversa, para la determinación experimental de estas constantes con gran precisión en la medida de lo permitido por las precisión de las determinaciones experimentales de conductividad(49).

En la práctica, gracias a la precisión de la tecnología actual, aparte de las frecuencias de excitación de la unión Josephson, que pueden ser medidas con niveles especialmente bajos de incertidumbre, tanto las tensiones discretas en dispositivos basados en el efecto Josephson (consistentes generalmente en agrupación de un gran número de uniones) como las conductividades transversales en configuraciones bidimensionales de gas de electrones pueden ser determinadas hoy día con una muy pequeña incertidumbre relativa, de manera que a las llamadas constantes R_K y K_J, definidas a través de las anteriores expresiones, se les han venido atribuyendo valores con muy baja incertidumbre (en 1990 ya se les atribuyeron valores recomendados respectivos “exactos” (sin incertidumbre), R_K-90= 25 812,807 Ω y K_J-90= 483 597,9 GHz/V) y en la última revisión del Sistema Internacional de Unidades(50), se les ha atribuido finalmente unos valores derivados de la consideración de valores exactos para las constantes h y e, en la forma:

En la práctica, pues, se ha optado, por “invertir” la utilidad de las medidas experimentales precisas de las constantes de Josephson y von Klitzing para la determinación de valores cada vez más precisos de la Constante de Planck en beneficio de poder fijar ésta última junto con la carga elemental para una definición acorde del kilogramo como unidad básica sólo en función de constantes fundamentales.

De hecho, la evolución de los valores convencionales adoptados para h como constante fundamental y sus correspondientes incertidumbres ha seguido un camino bastante accidentado hasta llegar al valor exacto definido en relación con la citada revisión del Sistema Internacional, \(h =6,6626\:070\:15\times 10^{-34}\:\:\textrm{J}\cdot \textrm{s}\) (exacto[51]. Un punto a resaltar es que, si bien la Constante de Planck está asociada (de acuerdo con su origen) a sistemas microscópicos, las determinaciones más precisas de la misma se han llevado a cabo generalmente a través de experimentos basados en procesos macroscópicos, mostrándose así una vez más su carácter de “constante universal” base de la conexión entre la Física Cuántica y los desarrollos tecnológicos contemporáneos.

Este hecho ha sido, precisamente, el utilizado para materializar el patrón del kilogramo como unidad fundamental en la revisión, con entrada en vigor en mayo de 2019, del Sistema Internacional de Unidades.

En efecto, sobre la base de la definición como constantes exactas de la propia Constante de Planck, h, la carga del electrón, e, y la velocidad de la luz en el vacío, c, se definió un procedimiento experimental basado en la utilización de la llamada “Balanza de Kibble”, utilizada con anterioridad de forma inversa, precisamente para determinar experimentalmente el valor de la Constante de Planck[52], hecho que se consiguió con una de las menores incertidumbres relativas registradas hasta el momento (1,0 x 10^-8), precisamente con la ayuda de la utilización de los métodos basados en la determinación de tensiones eléctricas mediante patrones basados la unión Josephson y resistencias eléctricas de efecto Hall mediante patrones basados en la constante de von Klitzing.

Analizando retrospectivamente los valores de las “constantes físicas fundamentales” con las que Planck construyó su “sistema natural” de unidades (tomados de publicaciones en los primeros años del siglo XX) en comparación con los valores actualmente postulados por la última revisión del Sistema Internacional de Unidades, obtenemos la siguiente tabla:

TABLA I:

Constante física	Valor comienzos       Siglo XX	Valor actual SI
Constante de Planck (h)	6,55×10-34 J·s   [53[	6,626 070 150×10-34 J·s
Constante de Boltzmann (k)	1,346×1023 J·K-1   [54]	1,380 649×1023 J·K-1
Velocidad de la luz (c)	299 860(10)×103 m·s-1  [55]	299 792 458 m·s-1
Constante gravitatoria (G)	6,6576(05)×10-11 m3·kg−1·s−2 [56]	6,674 08(31)×10-11 m3·kg−1·s−2  [57]
Carga del electrón (e)	1,591(1)×10-19 C  [58]	1,602 176 634×10-19 C
Constante de Avogadro (NA)	6,062(12)×1023 mol−1  [59]	6,022 140 76×1023 mol−1

En ella se puede observar que, a pesar de que en el caso de las dos constantes fundamentales de Planck (su propia constante y la constante de Boltzmann) los valores inicialmente estimados se apartan ligeramente (alrededor de 1% y 3% respectivamente) de los valores hoy día fijados como exactos, dichas desviaciones se pueden considerar como plenamente justificadas y asumibles teniendo en cuenta el hecho de que conjuntamente dieron lugar a un marco conceptual absolutamente novedoso para la Física y han venido siendo el objeto de una parte sustancial de la investigación científico-tecnológica del siglo XX y hasta nuestros días.

6. RECAPITULACIÓN

Recapitularemos, precisamente, en esta sección, sobre la importancia conceptual de la Teoría Cuántica y la constante de Planck (elemento fundamental, inherentemente ligado a su concepción y formulación) para la evolución y avances registrados en el conocimiento científico, en general, y en el desarrollo tecnológico asociado al mismo (hoy en día difícilmente separables).

Recordemos que la hipótesis de cuantización de la energía de Planck nació de forma aparentemente accidental y como un artificio matemático con motivo de su explicación de la distribución de energía en el espectro de radiación del “Cuerpo Negro” (1900), no siendo revelado hasta la interpretación de Einstein del efecto fotoeléctrico (1905) el carácter fundamental de dicha cuantización en términos de la constante h (E=hυ).

En aquel momento, no se estaba aún, ni mucho menos, ante la consideración de que el hecho de esta cuantización de la energía pudiera suponer una revolución significativa en el mundo de la Física, limitándose los investigadores de la época a considerar dichos efectos como manifestaciones (posiblemente inconexas) a las que se debería buscar explicación en el marco de las teorías conocidas. El espaldarazo fundamental a la apertura de un nuevo camino para la Física basado en la cuantización de magnitudes físicas (lo que posteriormente se ha venido llamando “discontinuidad cuántica”[60], lo proporcionó Bohr con la formulación de su modelo atómico y sus arriesgados postulados[61]. A través de los mismos, Bohr no sólo asumió de forma práctica la teoría del “Cuerpo Negro” de Planck, postulando directamente una interpretación de la cuantización de la energía en los procesos de absorción y emisión de radiación por los átomos, sino que, de forma muy significativa, introdujo la aplicación de lo que, posteriormente, en su discurso de aceptación del Premio Nobel, Planck denominaría su “cuanto de acción”.

En efecto, la introducción por Bohr del postulado de la cuantización del momento cinético del electrón en el átomo en términos del cuanto de acción de Planck (específicamente de ħ=h/2π) puso de manifiesto el significado más crucial de la constante h como constante fundamental, a saber, su carácter como cuanto elemental de acción[62] en función del cual fueron formulados los avances de Compton y de Broglie sobre comportamiento ondulatorio de las partículas (mencionados más arriba) que dieron finalmente lugar al desarrollo formal de la Teoría Cuántica introducido por Schrödinger y base de todos los desarrollos posteriores en este campo que han venido configurando decisivamente la Física de nuestros días, incluidos de forma muy destacada los de P.A.M. Dirac[63]) y R.P. Feynman[64].

De forma consistente, desarrollos científico-tecnológicos paradigmáticos como el LASER[65], el transistor[66] y los propios dispositivos basados en el efecto túnel (de los cuales la unión Josephson, anteriormente comentada, es un ejemplo notable) y en la cuantización de diversas magnitudes físicas en configuraciones características (efecto Hall cuántico, fenómenos de superfluidez[67], etc.) han venido, poco a poco, conformando el universo marcadamente tecnológico en el que vivimos, que, a pesar de nuestra general falta de percepción, es un mundo decisivamente influido por la Física Cuántica, en la cual la constante h juega un papel primordial desde diferentes puntos de vista, ya como parte del cuanto elemental de energía de radiación, ya como cuanto de acción asociable al momento cinético de las partículas y a sus propiedades electromagnéticas, ya formando parte de constantes físicas fundamentales, como es el caso especial de la constante de estructura fina (α), sin duda uno de los casos más especiales de constante física, con influencia decisiva en el fino ajuste físico que supone nuestra propia existencia[68].

Un papel que encuentra su origen, sin duda, en el que la propia constante de Planck juega en la descripción de los fenómenos físicos a todos los niveles, empezando por su influencia en el comportamiento de los átomos, los núcleos atómicos y los constituyentes más íntimos de la materia, una influencia decisiva que fue puesta claramente de manifiesto por R.P. Feynman en su formulación de una teoría avanzada de la Física Cuántica basada en la minimización de la acción[69] que muestra la Constante de Planck como una unidad de medida verdaderamente “natural”[70]. Aunque de forma mucho menos general y, desde luego, con un alcance mucho más limitado, dicha influencia global fue apuntada por Planck en su formulación del sistema de unidades basado en constantes universales, en el cual las constantes h y k jugaban un papel fundamental, indicando claramente la forma en la que dichas constantes fundamentales podrían configurar, en la forma tan ajustada en que lo hacen, el mundo en que vivimos.

En su sugerente artículo de 2016[71], P. Yang analiza de forma sistemática cómo la constante de Planck interviene en determinados aspectos concretos de la Física de nuestros días, y cómo un potencial cambio en el valor de dicha constante influiría en la propia constitución de nuestro Universo. En concreto, analiza la influencia de la constante sobre la potencial variación del espectro de la radiación electromagnética del “Cuerpo Negro” (el aspecto inicial en relación con el cual se postuló) y su delicado equilibrio con la gravitación en atmósferas estelares, sobre el tamaño de las órbitas y la energía en los átomos, sobre las propiedades del fotón como partícula y la longitud de onda (de de Broglie) atribuible a las ondas de materia, sobre la incertidumbre en la medida atribuible a la indeterminación de Heisenberg y sobre el valor del magnetón de Bohr, llegando a la conclusión de que, en definitiva, la constante de Planck no solamente tiene influencia directa sobre la Física del mundo microscópico (como era de esperar en función de su definición primigenia), sino que, por el contrario, tiene una influencia global sobre todo el Universo, también a nivel macroscópico, y cualquier variación de su valor, alteraría sustancialmente las interacciones entre la radiación y la materia y las propias condiciones de existencia del mismo.

De hecho, la propia relación existente entre la naturaleza de la radiación electromagnética (propagación de campos E y H) y el hecho de su emisión por todos los cuerpos con temperatura superior al cero absoluto de acuerdo con la ley de Planck, lleva de forma natural a pensar en la relación existente entre la Física Cuántica y el Electromagnetismo, implicando, por tanto, la necesidad de una interpretación estrictamente electromagnética para h. Gran parte del trabajo de P.A.M. Dirac y R.P. Feynman se ocupó precisamente de esta conexión, quedando la misma suficientemente establecida a través de su re-derivación de la ley de emisión de Planck en el contexto más general de la Electrodinámica Cuántica.

Sin embargo, y sin duda por razones prácticas y hasta cierto punto atribuibles a la necesidad de una introducción “pedagógica” de los conceptos cuánticos, parece existir aún una barrera infranqueable a la hora de tratar los fenómenos que admiten un tratamiento estrictamente clásico frente a los que requieren inexcusablemente una interpretación cuántica, siguiendo la actitud de “revolucionario conservador” con que fue calificado Planck en su momento al tratar de conservar la mayor parte del conocimiento acrisolado de la Física Clásica a pesar de la revolución evidente que implicaba la asunción como válida de su ley de emisión del “Cuerpo Negro”. Y en esta barrera aparece h como el factor de escala que determina la línea divisoria entre los fenómenos para los cuales la magnitud del “cuanto elemental de acción” es insignificante y aquellos para los cuales dicha magnitud es significativa. Sin embargo, hoy sabemos bien que dicha división es inapropiada y está condenada a la desaparición en vista de la interrelación real entre materia y radiación en el marco de la citada Electrodinámica Cuántica y las teorías de unificación de campos de fuerza (electromagnética, nuclear débil y nuclear fuerte) de las que, de momento, sólo la interacción gravitatoria parece quedar excluida[72].

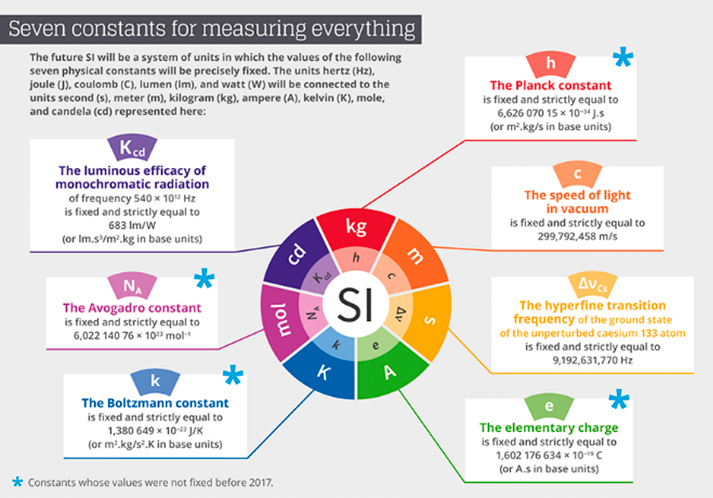
Por todas estas razones, y aún a pesar de que el resultado final no parece ser aún totalmente satisfactorio (sobre todo porque a nivel conceptual la Constante de Planck se halla presente en la Física de más fenómenos definitorios de unidades que los estrictamente ligados al kilogramo como unidad primaria)[73], no puede dejar de considerarse como un importante paso positivo la decisión del Comité Internacional de Pesos y Medidas del BIPM de basar el SI en constantes físicas fundamentales (ver figura 3), en la seguridad de que, progresando de esta forma, se estará cada vez más en la situación preconizada por Maxwell y Planck, de establecimiento de unidades verdaderamente universales “que retengan necesariamente su significado para todas las culturas, incluso las extraterrestres y no humanas”.

---

Referencias

1. PLANCK, M.: Carta de Max Planck a Robert Wood. 7 October 1931. Sources for the History of Quantum Physics. Recogida en ROBOTTI, N., BADINO, M: “Max Planck and the ‘Constants of Nature’”. Annals of Science, 58 (2001), 137-162.

2. MAXWELL, J.C.: “On the Dynamical Evidence of the Molecular Constitution of Bodies”. Transactions of the Sections, Notices and Abstracts of miscellaneous Communications to the Sections, Mathematics and Physics (British Association for the Advancement of Science, Liverpool) 1870, p. 7. Recogida en la obra “James Clerk. Maxwell: Trabajos Científicos”, compilada por J.M. Sánchez-Ron. CSIC (1998).

3. PLANCK, M.: “Über irreversible Strahlungsvorgänge”. Annalen der Physik, 306 (1900), 69-122.

4. PLANCK, M.: “Die Einheit der physikalische Weltbild”. Seminario Facultad de Ciencias Naturales de la Universidad de Leiden, 9 diciembre 1908. Verlag von S. Hirzel, Leipzig (1909).

5. CREPEAU, J.: “A Brief History of the T4 Radiation Law”. Proceedings HT 2009. 2009 ASME Summer Heat Transfer Conference. July 19-23, 2009, San Francisco, California USA. Paper HT2009-88060, pp. 1-7.

6. Ver, por ejemplo, el referido trabajo de ROBOTTI y BADINO (Referencia 1

7. PLANCK, M.: “The Genesis and Present State of Development of the Quantum Theory”. Nobel Lecture. June 2, 1920. Tambien en PLANCK, M.: “Die Entsehung und bisheringe Entwicklung der Quantentheorie” en Physikalische Abhandlungen und Vorträge, III. 121-136. Friedrich Vieweg & Sohn, Brandenburg (1958).

8. Ver Referencia 4.

9. KIRCHHOFF, G.R.: “Über den Zussamenhang zwischen Emission und Absorption von Licht und Wärme”. Monatsberichte der Königlichen Preussischen Akademie der Wissenschaften zu Berlin. (1859).

10. Ver, por ejemplo:
KUHN, T.S.: “La teoría del cuerpo negro y la discontinuidad cuántica, 1894-1912”. Alianza Universidad (1978).
WITTHAKER, E.T.: “A History of the Theories of Aether and Electricity”. Dover Publications (2017)
DUCK, I., SUDARSHAN, E.C.G.: “100 Years of Planck’s Quantum”. World Scientific (2000).
EL’YASHEVICH, M.A.: “From the Origin of Quantum Concepts to the Establishment of Quantum Mechanics”. Soviet Physics Uspekhi, 20 (1977), 656-682.

11. PLANCK, M.: “Zur Theorie des Gesetzes der Energieverteilung im Normalspectrum”. Verhandlungen der Deutschen Physikalischen Gesellschaft, 2 (1900) 237-245; después publicado como “Über das Gesetz der Energieverteilung im Normalspectrum”. Annalen der Physik, 4 (1901), 553-563.

12. LUMMER, O, PRINGSHEIM, E.: “Über die Strahlung des schwarzen Körpers für lange Wellen”. Annalen der Physik, 2 (1900), 163–180.

13. RAYLEIGH, F.R.S.: “The Law of Partition of Kinetic Energy”. Philosophical Magazine, Series 5, 49 (1900), 98-118; “Remarks upon the Law of Complete Radiation”. Ibid., Series 5, 49 (1900), 539-540; JEANS, J.H.: “On the Partition of Energy between Matter and Æther”. Ibid., Series 6, 10 (1905), 91-98.

14. WIEN, W.: “On the Division of Energy in the Emission-spectrum of a Black Body”, Philosophical Magazine, Series 5, 43 (1897), 214-220.

15. STEFAN, J.: “Über die Beziehung zwischen der Wärmestrahlung und der Temperatur”. Sitzungsberichte der Kaiserlichen Akademie der Wissenschaften. Mathematisch-Naturwissenschaftliche Classe, 79 (1879), 391-428.

16. BOLTZMANN, L.: “Über die mechanische Bedeutung des zweiten Hauptsatzes der Warmetheorie”. Sitzungsberichte der Kaiserlichen Akademie der Wissenschaften in Wien, Abt. II., LIII. (1866) 195-220; “Über die Beziehung zwischen dem zweiten Hauptsatze des mechanischen Wärmetheorie und der Wahrscheinlichkeitsrechnung, respective den Sätzen über das Wärmegleichgewicht”. Ibid., Abt. II., LXXVI. (1877), 373-435.

17. CLAUSIUS, R.: “The Mechanical Theory of Heat”. Taylor and Francis (1867).

18. PLANCK, M.: “Vorlesungen über die Theorie der Wärmestrahlung”. Verlag von Johann Ambrosius Barth (1906).

19. LORENTZ, H.A.: “The Theory of Electrons and Its Applications to the Phenomena of Light and Radiant Heat: A Course of Lectures Delivered in Columbia University, New York, in March and April, 1906”. B.G. Teubner (1909).

20. BOLTZMANN, L.: “Studien über das Gleichgewicht der lebendigen Kraft zwischen bewegten materiellen Punkten”. Sitzungsberichte der Kaiserlichen Akademie der Wissenschaften in Wien, Abt. II., LVIII. (1868), 517-560; “Weitere studien über das Wärmegleichgewicht unter Gasmolekülen”. Ibid., Abt. II., LXVI. (1872), 275–370.

21. PLANCK, M.: “Vorlesungen über die Theorie der Wärmestrahlung”. 2. Aufl.. Verlag von Johann Ambrosius Barth (1913).

22. Sin embargo, Boltzmann sí había expuesto con anterioridad. su teoría de formulación de la entropía en términos de la probabilidad de existencia de “complexiones” en su obra (Referencias previas 16). En cualquier caso, la inscripción de la fórmula que recoge esta dependencia figura como epitafio en su lápida fúnebre en el cementerio central de Viena. Como curiosidad, también en la lápida fúnebre de Planck en el cementerio de la ciudad de Gotinga (en el que también están enterradas figuras señeras ligadas a la Física Cuántica, como W. Heisenberg y M. Born) figura su constante en la forma: h=6,62 × 10^-34 W·s² (ver figura 2).

23. EHRENFEST, P.: “Über die physikalische Vorausetzungen der Planck’schen Theorie der irreversiblen Strahlungsvorgänge”. Sitzungsberichte der Kaiserlichen Akademie der Wissenschaften in Wien, Abt. II, CXIV. (1905), 1301-1314; “Bemerkung zu einer neuen Ableitung des Wienschen Verschiebungsgesetzes”. Physikalische Zeitschrift, 7 (1906), 527–528; “Zur Planckschen Strahlungstheorie”. Ibid., 7 (1906), 528–532.

24. EINSTEIN, A.: “Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt“. Annalen der Physik, 17 (1905), 132–148. En uno de sus cuatro trabajos fundamentales publicados en 1905, Albert Einstein adaptó el postulado de Planck para explicar el efecto fotoeléctrico proponiendo que la energía de los fotones a su vez estaba cuantizada, y que la cuantización no era una propiedad exclusiva de los osciladores microscópicos.

25. BOHR, N.: “On the Constitution of Atoms and Molecules”. Philosophical Magazine, Series 6, 26 (1913), 1-25. El postulado de Planck fue también usado para explicar el espectro de emisión del átomo de hidrógeno y derivar el valor correcto de la Constante de Rydberg.

26. En realidad fue N. Bohr en la formulación de su modelo atómico el que atribuyó por primera vez a ħ=h/2p el carácter de momento cinético cuantizado, pero fue el propio M. Planck, en su discurso de aceptación del Premio Nobel en 1918 (referencia 7) quien constató y puso de manifiesto la verdadera importancia del concepto de cuanto de acción y su carácter novedoso. En palabras del propio Planck:  “…la derivación de la ley de radiación se basó en un concepto físico notable. En este caso, el cuanto de acción, un concepto completamente novedoso, del que nunca se había oído hablar, debe jugar un papel fundamental en la Física que parece estar llamado a hacernos revisar todas nuestras concepciones físicas…”.

27. COMPTON, A.H.: “A Quantum Theory of the Scattering of X-rays by Light Elements”. Physical Review, 21 (1923), 483-502.

28. DE BROGLIE, L.: “A Tentative Theory of Light Quanta”. Philosophical Magazine, Series 6, 47 (1924), 446-458; Este artículo había sido precedido por la Tesis del autor, defendida también en 1924 y publicada un año después: “Recherches sur la Théorie des Quanta”. Annales de Physique, 10 (1925), 22–128.

29. EINSTEIN, A.: “Zur Elektrodynamik bewegter Körper“. Annalen der Physik, 17 (1905), 891-921.

30. Teoría fundacional de la Mecánica Cuántica Ondulatoria publicada en cuatro partes: SCHRÖDINGER, E.: “Quantisierung als Eigenwertprobem”, Annalen der Physik, 384 (1926) 361-376; Ibid., 384 (1926) 489-527; Ibid., 385 (1926) 437-490; Ibid., 386 (1926), 109-139. El mismo Schrödinger publicaría simultáneamente un artículo en el que mostraba la equivalencia de su desarrollo con el realizado por W. Heisenberg, M. Born y P. Jordan (Teoría de la Mecánica Cuántica basada en álgebra de matrices): SCHRÖDINGER, E.: “Über das Verhältnis der Heisenberg-Born-Jordanschem Quantenmechanik zu der meinem”. Annalen der Physik, 384 (1926) 734-756.

31. Ver Referencia 4.

32. PLANCK, M.: “Über irreversible Strahlungsvorgänge. 5. Mitteilung”. Sitzungsberichte der Preussischen Akademie der Wissenschaften (1899). Publicado posteriormente como Annalen der Physik, 306 (1900), 69-122 (Referencia 3).

33. STONEY, G.J.: “On the Physical Units of Nature”. Report to the British Association. 44^th meeting. (1874). Publicado posteriormente en Philosophical Magazine, 11 (1881), 381-390. Fue precisamente con ocasión de esta búsqueda de “constantes universales” cuando Stoney proporcionó una nueva interpretación para las leyes de la electrolisis y descubrió “una cantidad definida de electricidad” a la que denominó “electrón” y con arreglo a la cual los átomos parecían combinarse entre sí.

34. DRUDE, P.: “Über Fernewirkungen”. Beilage zu den Annalen der Physik und Chemie. Band 62, 1, Neue Folge, (1897), S. I–XLIX.

35. En realidad, debido a la verdadera naturaleza del cuanto de acción de Planck (mejor representado dimensionalmente por ħ=h/2π), se ha consolidado la unidad de carga \(q_{p} = \left (\frac{c\hbar}{k_{e}} \right )^\frac{1}{2}= (4\pi \varepsilon_{0}c\hbar)^\frac{1}{2} \cong1,87\:\: \times\:\: 10^{-18}\) C, curiosamente valor relativamente cercano al de la carga elemental electrónica.

36. En Física, la acción es la magnitud que expresa el producto de la energía implicada en un proceso por el tiempo que éste dura. Se trata de una magnitud física que no es directamente medible, aunque puede ser calculada a partir de cantidades medibles. En el marco de la Física Cuántica, la acción está cuantizada siendo la unidad elemental la constante reducida de Planck ħ=h/2π . Las ecuaciones de evolución de los sistemas, tanto en Física Clásica como en Física Cuántica se derivan a partir del Principio de Mínima Acción, formulado por Pierre-Louis Moreau de Maupertuis en 1744.

En lo referido a la dimensionalidad correcta de la acción que debe figurar en las fórmulas físicas, a pesar de que la constante h según la formuló el propio Planck tiene las dimensiones de Energía-tiempo (acordes a la definición), cuando dicha constante forma parte de expresiones físicas en las cuales figura el momento cinético (generalmente cuantizado) o ha de compatibilizarse con otras magnitudes angulares (en las cuales la dimensión natural es el radián y no el ciclo) la constante requerida es la citada ħ=h/2π  (de aparente idéntica dimensionalidad que la constante h:

ħ [=] m .kg m s^-1 [=] kg m² s^-2.s [=] J.s, igualmente )

Para una discusión sobre este aspecto de la dimensionalidad apropiada para las expresiones físicas en las que deba figurar la constante de Planck, pueden consultarse los artículos:

FREEMAN, G.R.: “SI Units of Frequency, Angular Velocity, Planck’s Constant and ħ”. Metrologia, 23 (1986/87), 221-222.
MOHR, P.J., PHILLIPS, W.D.: “Dimensionless units in the SI”. Metrologia, 52 (2015) 40–47.
MILLS, I.: “On the units radian and cycle for the quantity plane angle”. Metrologia, 53 (2016) 991–997.
BUNKER, P.R. y otros: “The Planck Constant and its Units”. Journal of Quantitative Spectroscopy & Radiative Transfer, 237 (2019) 106594:1-3.

37. Bureau International de Poids et Mesures: “Le Système International d’Unités”. 9^ème Edition (2019).

38. LÉVY-LEBLOND, J.M.: “On the Conceptual Nature of the Physical Constants”. Rivista del Nuovo Cimento, 7 (1977), 187-214.

39. MILLIKAN, R.A.: “A Direct Determination of “h””. Physical Review, 4 (1914), 73-75 ; “A Direct Photoelectric Determination of Planck’s h“. Ibid., 7 (1916), 355-388.

40. CLADÉ, P. y otros: “State of the art in the determination of the fine-structure constant and the ratio h/m_u”. Comptes Rendus de Physique, 20 (2019), 77–91.

41. Ver, por ejemplo:
KUSCH, P., FOLEY, H.M.: “The magnetic moment of the electron”. Physical Review, 74 (1948), 250-263.
BOVEY, F.A.: “Nuclear Magnetic Resonance Spectroscopy”, 2ª Ed. Academic Press (1988).
NOVITSKI, E.M.: “Apparatus and Methods for a New Measurement of the Electron and Positron Magnetic Moments”. PhD Dissertation. Harvard University (2017). http://nrs.harvard.edu/urn-3:HUL.InstRepos:39945340.

42. Ver, por ejemplo:
DRYZEK, J., RUEBENBAUER, K.: “Planck’s Constant Determination from Black-Body Radiation”. American Journal of Physics, 60 (1992), 251-253.
CHECCHETTI, A., FANTINI, A.: “Experimental Determination of Planck’s constant using Light Emitting Diodes (LEDs) and Photoelectric Effect”. World Journal of Chemical Education, 3 (2015), 87-92.
USMAN, A. y otros: “A tutorial for laboratory determination of Planck’s constant from the Planck radiation law”.  Latin-American Journal of Physics Education, 3 (2009), 246-252.

43. JOSEPHSON, B.D.: “Possible New Effects in Superconductive Tunnelling”. Physical Review Letters, 1 (1962), 251-253.

44. VON KLITZING, K. y otros: “New Method for High-Accuracy Determination of the Fine-Structure Constant based on Quantized Hall Resistance”. Physical Review Letters, 45 (1980), 494-497.

45. Ver, por ejemplo:
DÍAZ DE AGUILAR, J. y otros: “Metrología eléctrica cuántica y digital”. Revista e-Medida (2018). <https://www.e-medida.es/numero-14/metrologia-electrica-cuantica-y-digital/>; SANMAMED, Y.A., DÍAZ DE AGUILAR, J.: “La definición del amperio en el SI Revisado”. Revista e-Medida (2018)<https://www.e-medida.es/numero-15/la-definicion-del-amperio-en-el-si-revisado/>; NEWELL, D.B.: “A more fundamental International System of Units”. 67 (2014), 35-41.
JECKELMANN, B., PIQUEMAL, F.: “The Elementary Charge for the Definition and Realization of the Ampere”. Annalen der Physik, 531 (2019), 1800389:1-10.

46. COOPER, L.N.: “Bound Electron Pairs in a Degenerate Fermi Gas”. Phys. Rev. 104 (1956), 1189-1190; IONOV, A.I.: “Resonance Tunneling of Cooper Pairs in a Superconductor–Polymer–Superconductor Josephson Junction”. Journal of Experimental and Theoretical Physics, 116 (2013), 834–837.

47. KOHLMAN, J., BEHR, R.: “Development of Josephson Voltage Standards”. In Superconductivity–Theory and Applications. InTech (2011).

48. PASHITSKII, E.A.: “Cooper Pairing of Two-Dimensional Electrons in a Quantizing Magnetic Field and the Fractional Quantum Hall Effect”. Low Temperature Physics, 25 (1999), 690-701.

49. BACHMAIR, H. y otros: “The von Klitzing Resistance Standard”.  Physica E, 20 (2003), 14-23.

50. Ver Referencia 37.

51. Ver, por ejemplo:
STEINER, R.: “History and Progress on Accurate Measurements of the Planck Constant”. Reports on Progress in Physics, 76 (2013), 016101:1-46.
POSSOLO, A. y otros: “Evaluation of the Accuracy, Consistency, and Stability of Measurements of the Planck Constant Used in the Redefinition of the International System of Units”. Metrologia, 55 (2018), 29-37.
NEWELL, D.B. y otros: “The CODATA 2017 values of h, e, k, and N_A for the revision of the SI”. Metrologia, 55 (2018), L13–L16.
Karshenboim, S.G.: “Accurate Determination of the Values of Fundamental Physical Constants: The Basis of the New “Quantum” SI Units”. Physics of Particles and Nuclei, 49 (2018), 213–248.
NIST: “2018 CODATA Recommended Values of the Fundamental Constants of Physics and Chemistry”. NIST SP 959 (June 2019). https://physics.nist.gov/cuu/Constants/index.html.
PAVESE, F.: “The New SI and the CODATA Recommended Values of the Fundamental Constants 2017 Compared with 2014, with a Comment to ‘Possolo et al., Metrologia 55 (2018) 29’”. ArXiv physics.data-an 1512.03668v5 (2019).

52. Ver, por ejemplo:
KIBBLE, B.P. y otros: “A Realization of the SI Watt by the NPL Moving-coil Balance”.   Metrologia, 27 (1990), 173-192.
STOCK, M.: “The Watt Balance: Determination of the Planck Constant and Redefinition of the Kilogram”. Philosophical Transactions of the Royal Society A, 369 (2011), 3936-3953.
SCHLAMMINGER, S. y otros: “Determination of the Planck Constant using a Watt Balance with a Superconducting Magnet System at the National Institute of Standards and Technology”. Metrologia, 51 (2014), S15–S24.
HADDAD, D. y otros: “A Precise Instrument to Determine the Planck Constant, and the Future Kilogram”. Review of Scientific Instruments, 87 (2016), 061301:1-14.
THOMAS, M.  y otros: “A determination of the Planck Constant using the LNE Kibble Balance in Air”. Metrologia, 54 (2017), 468-480.
SCHLAMMINGER, S. HADDAD, D.: “The Kibble Balance and the Kilogram”. Comptes Rendus de Physique, 20 (2019), 55-63.

53. Ver Referencia 11.

54. Ibid.

55. ROSA, E.B., DORSEY, N.E.: “A New Determination of the Ratio of the Electromagnetic to the Electrostatic Unit of Electricity”. Bulletin of the Bureau of Standards, 3 (1907), 433-540; continuado en Ibid., 541-604.

56. BOYS, C.V.: “On the Newtonian Constant of Gravitation”. Philosophical Transactions, 186 (1895), 1-72.

57. MOHR, P.J. y otros.: “CODATA Recommended Values of the Fundamental Physical Constants: 2014”. Review of Modern Physics, 88 (2016), 035009:1-73.

58. MILLIKAN, R.A.: “On the Elementary Electric Charge and the Avogadro Constant”. Physical Review, 2 (1913), 109-143.

59. Ibid.

60. Ver Referencia 10.

61. Ver Referencia 25.

62. Ver Referencias 26, 35 y 36.

63. DIRAC, P.A.M.: “The Principles of Quantum Mechanics”. 4ª Ed. Oxford University Press (1958); “The Quantum Theory of the Emission and Absorption of Radiation”, Proceedings of the Royal Society, A114 (1927), 243-265; “Relativistic Quantum Mechanics”. Proceedings of the Royal Society, A136 (1932), 453-464.

64. FEYNMAN, R.P.: “The Theory of Positrons”. Physical Review, 76 (1949), 749-759; “Space-Time Approach to Quantum Electrodynamics”. Physical Review, 76 (1949), 769-789; “Mathematical Formulation of the Quantum Theory of Electromagnetic Interaction”. Physical Review, 80 (1950), 440-457.

65. Ver una revisión crítica en: OCAÑA, J.L.: “El LASER: Paradigma de la Física Cuántica e Instrumento Clave para el Desarrollo Científico-Tecnológico”. Real Academia de Doctores de España (2019).<https://www.radoctores.es/doc/OCAÑA%20MORENO,%20Jose%20Luis_discurso%20de%20ingreso.pdf>.

66. SHOCKLEY, W.: “The Path to the Conception of the Junction Transistor”. IEEE Transactions on Electron Devices, ED-31 (1984), 1523-1546; ROSS, I.M.: “The Invention of the Transistor”. Proceedings of the IEEE, 86 (1998), 7-28.

67. The Royal Swedish Academy of Sciences: “The Nobel Prize in Physics 1996”. Advanced information. <https://www.nobelprize.org/prizes/physics/1996/advanced-information/>.

68. Ver, por ejemplo:
XIAO, K.: “The Fine Structure Constant and Interpretations of Quantum Mechanics”. European Journal of Theoretical Physics, 26 (2012) 135-146;
UZAN, J.P., LECLERCQ, B.: “The Natural Laws of the Universe: Understanding Fundamental Constants”. Springer (2008).

69. FEYNMAN, R.P.: “The Principle of Least-Action in Quantum Mechanics”. PhD Dissertation. Princeton University (1942).

70. QUINCEY, P.: “Planck’s Constant as a Natural Unit of Measurement”. Physics Education, 48 2013), 597-600.

71. YANG. P.: “How Does Planck’s Constant Influence the Macroscopic World?”. European Journal of Physics, 37 (2016), 1-9.

72. DAVIES, P.: “The Forces of Nature”, 2ª Ed. Cambridge University Press (1986).

73. En concreto, y principalmente, se considera necesaria una definición más apropiada y directa del kilogramo como unidad primaria, sin el recurso a la simple fijación de la Constante de Planck; se considera asimismo mejorable el proceso de materialización práctica de la unidad, que al final depende de medidas locales de la aceleración de la gravedad, en vez de haber hecho figurar la constante universal G (a pesar de su aun relativamente importante nivel de incertidumbre relativa); a pesar de que ello tiene ventajas desde un punto de vista práctico, se considera redundante desde un punto de vista conceptual la definición de la candela como unidad primaria, toda vez que puede referirse directamente a unidades de energía y, además, debería también redefinirse con ayuda de la Constante de Planck, utilizando, así, el marco originario de aplicación de la constante; se desdibuja el camino que liga la unidad de masa con la metrología de fuerza en su estado actual; falta de relación aparente entre la unidad de cantidad de materia (mol) y la masa;……A pesar de que en la última definición se ha hecho un esfuerzo por corregir algunos temas planteados previamente, algunas de estas dificultades, tanto conceptuales como referidas a implantación práctica, subsisten aún y han sido puestas de manifiesto en algunas referencias tales como:
FOSTER, M.P.: “The next 50 years of the SI: a review of the opportunities for the e-Science age”. Metrologia, 47 (2010), R41-R51.
PRICE, G.: “A skeptic’s review of the New SI”. Accreditation and Quality Assurance, 16 (2011), 121-132.
MEDINA, M.N.: “2019: la definición del kilogramo en el SI revisado”. Revista e-Medida (2019); <https://www.e-medida.es/numero-14/2019-la-definicion-del-kilogramo-en-el-si-revisado/>.

74. PIGENET, Y.: “Ces constantes qui donnent la mesure”. CNRS News (2018). <https://lejournal.cnrs.fr/articles/ces-constantes-qui-donnent-la-mesure>.