Francisco González de Posada
Resumen
Se presenta la elaboración de una nueva teoría de las magnitudes físicas (primera de una serie de cuatro teorías matemáticas: de las magnitudes físicas, de las leyes físicas, de las teorías físicas y del concepto de dimensión), que conduce, de manera hipotético-deductiva, según el deseo frustrado de los principales autores de Análisis dimensional, al concepto de dimensión de manera rigurosa.
En este artículo se describen los elementos básicos de una teoría matemática de las magnitudes físicas, primera de las cuatro teorías antes indicadas que ha desarrollado el autor.
Palabras claves: análisis dimensional, magnitud, cantidad, unidad, medida, dimensión, Bridgman, Palacios, Bunge.
Abstract
The elaboration of a new theory of physical magnitudes is presented (first in a series of four mathematical theories: of physical magnitudes, of physical laws, of physical theories and of the concept of dimension), which leads, in a hypothetico-deductive manner, according to the frustrated desire of the main writers of Dimensional Analysis, to the concept of dimension in a rigorous manner.
This article describes the basic elements of a mathematical theory of physical magnitudes, the first of the four theories mentioned above that the author has developed.
Keywords: dimensional analysis, magnitude, quantity, unit, measure, dimension, Bridgman, Palacios, Bunge.
Contexto: la necesidad de una Teoría Dimensional
Pueden destacarse las manifestaciones de tres de los principales autores en la cuestión tradicional de la deficiencia del Análisis Dimensional1, considerados clásicos.
P.W. BRIDGMAN (1931): Dimensional Analysis, Yale University Press, New Haven (AMS, 1978). Premio Nobel, considerado ‘fundador’ del Análisis Dimensional como disciplina científica. En el Prefacio:
“The growing use of the methods of dimensional analysis in technical physics, as well as the importance of the method in theoretical investigations, makes it desirable that every physicist should have this method of analysis at his command. There is, however, nowhere a systematic exposition of the principles of the method. Perhaps the reason for this lack is the feeling that the subject is so simple that any formal presentation is superfluous. There do, nevertheless, exist important misconceptions as to the fundamental character of the method and the details of its use. These misconceptions are so widespread, and have so profoundly influenced of many speculations […]
[…] to emphasize the points concerning which there is the most common misunderstanding, such as the nature of a dimensional formula, the proper number of fundamental units, and the nature of dimensional constants”.2
En este texto se señala en negritas el término método, carácter propio del Análisis Dimensional clásico, que, como él afirma, está falto de una exposición sistemática. Esta deficiencia se pretende superar con la Teoría Dimensional concebida de la que aquí se exhibe la primera de las teorías matemáticas que la integran.
J. PALACIOS (1956): Análisis Dimensional. Espasa-Calpe, Madrid; 2ª ed. 1964, págs. 11 y 12.
“Con su ya vieja historia, con su utilidad manifiesta, que se revela, no sólo en el campo de la Física teórica, sino en problemas técnicos, en los ensayos con modelos reducidos de aviones, buques, y construcciones hidráulicas y, sobre todo, con la intervención de los físicos más eminentes, sería de esperar que el Análisis Dimensional estuviese ya asentado sobre bases sólidas, y que hubiese unanimidad acerca de la manera de emplearlo. Lejos de ser así, los físicos se hallan divididos en grupos cuyas opiniones discrepan en lo más esencial: en el concepto mismo de dimensión.”
M. BUNGE (1971) “A Mathematical Theory of the Dimensions and Units of Physical Quantities” en Bunge (ed.): Problems in the Foundations of Physics. New York: Springer-Verlag.
“Every physicist knows to perform a dimensional analysis and how to calculate the units of a dimensionally complex magnitude, but no theory proper has hitherto justified these operations. Worse: the two concepts are often mixed up. Even worse: they are frequently “defined” by reference to measurement operations […]
Dimensional analysis is an established Branch of the foundations of physics. However it is more of a loose collection of concepts, theorems and rules than a hypothetico-deductive system. It is much in the same state as HEAVISIDE’s “operational calculus” before it was legitimated by the theory of Laplace transforms. So much so, that dimensional analysis does not even supply a mathematical analysis of the very notion of a dimension”3.
De estos juicios críticos tan severos acerca del estado en que se encuentra el Análisis Dimensional se destacan los dos aspectos principales que pregona mi maestro Mario Bunge, en tanto que consideraciones marco.
- Ninguna teoría ha justificado adecuadamente los conceptos básicos, que se mezclan con frecuencia.
- El Análisis Dimensional ni tan siquiera aporta un análisis matemático de la propia noción de dimensión.
Estas claras consideraciones nos invitaron a ponerle remedio. Así, se pretende disponer de una fundamentación sólida del concepto de dimensión de una magnitud física. Para ello resulta necesario proporcionar un tratamiento teórico completo y riguroso que hasta ahora no existía. Con esta finalidad se construye un sistema hipotético-deductivo constituido por cuatro teorías matemáticas concatenadas entre sí:
- Teoría de las magnitudes físicas;
- Teoría de las leyes físicas;
- Teoría de las teorías físicas; y
- Teoría del concepto de dimensión.
Una vez que se expongan sintéticamente las cuatro teorías, todos los conceptos dimensionales quedarán ubicados en un marco estructurado lógicamente. Estas cuatro teorías de fundamentos de física constituyen la Teoría Dimensional.
En este artículo se desarrolla la primera de estas teorías, una ‘nueva’ Teoría de las magnitudes físicas.
1. Introducción
Entre las notas que caracterizan la teoría de las magnitudes físicas que se desarrolla en este artículo pueden destacarse las siguientes.
a) Relativas a la teoría.
Primera. Es una teoría primordial en el sentido de que es, de hecho, con propiedad, la correspondiente a las únicas magnitudes físicas que con consideración de tales -es decir, de magnitudes- utiliza la Física. Es, en sí misma y conceptualmente, la teoría por excelencia. (Otro tema sería el de la calidad de las exposiciones que se han publicado a lo largo de la historia).
Segunda. Es una teoría general ya que (pretendidamente al menos) es -o se considera como- de validez general para todas las magnitudes que propiamente considera la Física como tales.
Tercera. Es, en sí misma, una teoría (necesariamente) única de las magnitudes que existen (en el sentido de las magnitudes propiamente dichas). Obviamente esto no quiere decir que sólo pueda exponerse de una manera, ni mucho menos que la que aquí se exhibe sea ni la única, ni la primera, ni la mejor.
Cuarta. Es una teoría prioritariamente matemática.
b) Relativas a las ‘magnitudes’ a las que se refiere y aplica.
Primera. Son las magnitudes físicas usuales, las que considera la ciencia física desde su constitución como tales magnitudes y que sigue vigente, en tanto que criterio rector según la IUPAP (Unión Internacional de Física Pura y Aplicada).
Segunda. Estas magnitudes físicas se consideran (pretendidamente, en realidad se consideraban y se consideraron) generales; es decir, que todas son análogas y tratadas de acuerdo con una teoría única.
Tercera. Sustantiva y propiamente son magnitudes clásicas, en el sentido de que son las que utiliza la Física clásica.
Estas características no impiden que en otros ámbitos de la Física existan o puedan existir magnitudes que en sí mismas sean clásicas, aunque se integren en teorías no clásicas.
En resumen, se exhibe en este capítulo, en síntesis apretada, lo que podría denominarse más extensamente: teoría matemática primordial de las magnitudes físicas clásicas.
2. Conceptos fundamentales: magnitud, cantidad, unidad y medida
2.1. Ideas iniciales
La Teoría Dimensional, el Análisis Dimensional, la Teoría de la Medida y la Física en conjunto utilizan cuatro conceptos: magnitud, cantidad, unidad y medida, que poseen, a mi juicio, la condición de fundamentales. Por ello considero estrictamente necesario dedicarles una atención especial. Más aún, teniendo en cuenta que es difícil encontrar un texto de Física en el que se traten temas relacionados con ellos, de la naturaleza específica o general que fueren, en los que se distingan nítidamente como distintos y se caractericen adecuadamente.
El objeto de este punto consiste, pues, en caracterizarlos tanto como nos resulte posible, de modo que se distingan perfectamente entre sí y de otros próximos -como son los conceptos de patrón y medición-.
En primer lugar, conviene destacar unas ideas relativas a la naturaleza de conceptos.
Primera. Son conceptos, en consecuencia, esencialmente entes ‘ideales’, no propiamente ‘realidades’.
Segunda. Son conceptos de naturaleza prioritariamente matemática.4
Tercera. Son, por tanto, conceptos matematizables (y en esta condición, como en las restantes, deben caracterizarse “tanto y tan bien como se puedan”).
Cuarta. Son cuatro conceptos nítidamente diferentes.
En segundo lugar, conviene destacar también unas ideas relativas al papel que desempeñan en tanto que se consideran conceptos fundamentales.
Primera. Son conceptos fundamentales de la Teoría Dimensional, del Análisis Dimensional y de la Teoría de la Medida.
Segunda. Son conceptos fundamentales de/en/para toda la Física.
Y, en tercer lugar, desde una perspectiva pedagógica y para lectura de textos de Física, se considera conveniente la adquisición de una primera impresión conjunta e individual de estos conceptos que permita conocer y diferenciar con suficiente precisión los cuatro conceptos, tantas veces diversamente confundidos.
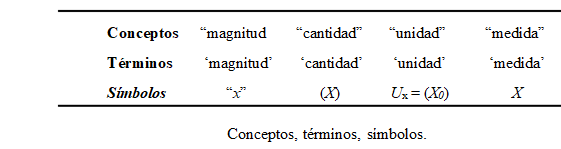
2.2. Conceptos, términos, símbolos
En el cuadro adjunto se explicitan, en la línea sugerida por Mario Bunge5, diversos niveles que deben distinguirse para saber de qué se trata. En síntesis: el concepto en sí mismo -el qué del que se habla o escribe-, el término lingüístico que se utiliza para saber de qué se habla o escribe -del concepto-, y el símbolo matemático (en su caso, como es el presente) que representa al qué -al concepto-.
2.3. Caracterización introductoria: primeras notas sustantivas diferenciadoras6
El concepto de cantidad7 ocupa el papel primordial desde una perspectiva lógica. Es, entre los cuatro, el concepto primario (los otros de alguna manera o se derivan exclusivamente de él o son consecuencia, entre otros elementos, de él) y el único propiamente físico (tiene referente real directo, se refiere directamente a algo -supuestamente al menos- existente en la Naturaleza). Se representa por símbolos de la forma (X), (A).
El concepto de unidad es cualquier cantidad elegida arbitrariamente; es decir, elegida -destacada-, pero una cantidad cualquiera (en la formalización matemática se añadirá ‘no nula’). No tiene sentido intrínseco. La unidad es un concepto teórico; en la práctica se usan patrones o unidad-patrón, con el sentido de utilidad que es diferente a un concepto teórico. Formalmente toda cantidad (salvo la cantidad nula) puede considerarse como unidad; es decir, simbólicamente:
\(U_{x}=\left ( X \right ); U_{x}^{\prime}=\left ( X^{\prime} \right );U_{x}^{\prime\prime}=\left ( X^{\prime\prime} \right )\)
(1)
El concepto de medida8 se construye como relación entre la cantidad que se mide (que es un invariante, por el postulado de invariancia magnitudinal) y la unidad elegida (‘arbitraria’ pero ‘una’), relación matemática (proporción aritmética, de momento) que se presupone siempre posible y cuyo resultado es un número real. Estos postulados y operaciones, ahora sólo referidos, se explicitarán con precisión y detalles en el punto “4. Postulados”, dedicado a la matematización. Por ahora baste expresar la relación clásica, entre una cantidad y sus medidas respecto de diferentes unidades, siguiente:
\(\left ( A \right )= A U_{a}=A^{\prime}U^{\prime}{a}=A^{\prime\prime}U^{\prime}{a}= …\)
(2)
de la que se deduce la importante ecuación entre medidas y unidades:
\(\frac{A}{A^{\prime}}=\frac{U_{a}^{\prime}}{U_{a}}\)
(3)
que suele expresarse diciendo que “las medidas son inversamente proporcionales a las unidades”.
El concepto de magnitud se refiere a la clase de cantidades cualitativamente idénticas: es el conjunto de cantidades reales, posibles y concebibles de idéntica naturaleza.
\(“a”= \{ (A_{1}), (A_{2}), (A_{3}), … \}\)
(4)
Estas primeras notas sustantivas, caracterizadoras y diferenciadoras de los cuatro conceptos fundamentales, pueden sintetizarse, a modo de resumen conjunto, de la manera siguiente:
- Cantidad: concepto primario (con referente, en principio, real).
- Magnitud: concepto cualitativo, de clase.
- Unidad: cantidad arbitraria (concepto teórico; diferente del patrón, o unidad-patrón).
- Medida: número real (concepto teórico; diferente de la medición concreta, fruto ésta de un proceso u operación).
2.4. Ejemplo
Un sencillo ejemplo -referido a una barra de tiza- facilitará la comprensión y diferenciación de estos conceptos fundamentales. Se describe en el siguiente cuadro.
| Objeto (material o no) soporte: | la barra de tiza (objeto) |
|---|---|
| Cantidad | 10 cm |
| Magnitud | longitud (abstracto) |
| Unidad | cm |
| Medida | 10 |
3. El modelo magnitudinal clásico
3.1. Consideraciones iniciales
En el punto anterior se han caracterizado básicamente y diferenciado nítidamente cuatro conceptos fundamentales distintos pero correlacionados.
Aceptada la concepción establecida en el punto precedente, surge una segunda cuestión, de importancia capital, que se resume y expresa claramente en las preguntas siguientes: ¿todas las magnitudes físicas son así?, ¿a todas puede aplicárseles ese determinado cuarteto de conceptos? y/o ¿cuántos tipos (distintos) de magnitudes físicas hay?
La Física es una ciencia cuyo referente es la Naturaleza, pero sin que sea, de ninguna manera, la Naturaleza. Las magnitudes físicas lo son de la Física -siempre y sólo, por su propia esencia conceptual- no de la Naturaleza. Pero se refieren, ¡eso sí!, a propiedades de la Naturaleza.
En el ámbito de la Física, en el que tienen sentido las preguntas, y referido a sus capítulos relativos a la Física Clásica, a la Teoría de las Magnitudes, a la Teoría de la Medida y al de la visión fundamental establecida por la Unión Internacional de Física Pura y Aplicada (IUPAP) en los documentos compilados por la Comisión de Símbolos, Unidades, Nomenclatura, Masas atómicas y Constantes fundamentales, puede afirmarse lo siguiente.
Primero. Existe una concepción magnitudinal, un tipo de magnitudes, un modelo magnitudinal.
Segundo. Este modelo es esencialmente único; en otras palabras, existe uno y sólo uno. Hay matices y clasificaciones de las magnitudes, pero son complementarias, es decir, adjetivas, pero no sustantivas.
Tercero. Algo más. En este modelo –la “Teoría de las Magnitudes”-, con este modelo y para este modelo se crea y desarrolla el concepto de dimensión.
3.2. Notas en torno al concepto global de magnitud
Una magnitud física puede considerarse como la clase o conjunto de las cantidades que pueden medirse respecto de una cantidad arbitrariamente elegida como unidad, es decir, considerada en sentido amplio integrador de los cuatro conceptos fundamentales. Bajo esta perspectiva conviene delimitar su campo propio con el mayor rigor posible. He aquí unas notas capitales.
Primera. Una magnitud es un “concepto” concebido, en principio, ‘en’ y ‘para’ una teoría física determinada. (Se dice ‘en principio’ desde una perspectiva lógica, lo que no quiere decir que sus creadores o utilizadores no pretendieran mucho más e incluso que algunas magnitudes se hayan utilizado en diversas o en muchas teorías físicas).
Segunda. No obstante, también puede constatarse que un único ‘término’ (de la Física) puede designar diferentes “conceptos” (de la Física) en distintas teorías físicas.
Tercera. Una magnitud física se caracteriza no sólo intrínsecamente -por sí sola- en/para ‘una’ teoría física, sino que, además, se integrará de alguna manera en las leyes de dicha teoría física.
3.3. Caracterización de una magnitud
Dos aspectos fundamentales de distinta índole son estrictamente necesarios para caracterizar una determinada magnitud física. Son los siguientes:
- Su significado físico-filosófico; es decir, su caracterización epistémica, cualitativa, su relación con el referente.
- Su naturaleza físico-matemática; es decir, la caracterización de y para: 1) su esencialidad; 2) su cuantificabilidad (y medibilidad); y 3) su relacionalidad (legal y de derivación de magnitudes secundarias).
El primer aspecto, su significado físico-filosófico, es esencialmente diferente para cada magnitud; el segundo, su naturaleza físico-matemática, pretende ser esencialmente idéntico para todas ellas. De este aspecto físico-matemático, o del aspecto matemático del ente físico, se trata en la Teoría Dimensional.
El desarrollo total de las cuatro teorías se expone en la tesis doctoral que se ha propuesto a la Universidad de Castilla-La Mancha: Teoría Dimensional. Teoría algebraica de las magnitudes físicas: antecedentes, construcción, extensiones y aplicaciones.
Notas al pie
1 Esta situación de falta de una elaboración teórica se extiende al ámbito meteorológico. Lógicamente se presentan algunos conceptos, términos y notaciones que difieren, por ejemplo, con los utilizados en el VIM (Vocabulario Internacional de Términos Metrológicos).
2 Traducción: “El uso creciente de los métodos de análisis dimensional en física técnica, así como la importancia del método en investigaciones teóricas, hace deseable que todo físico domine este método de análisis. Sin embargo, no se encuentra en ningún sitio una exposición sistemática de los principios de este método. Quizá la razón de esta falta radique en la sensación de que la disciplina es tan simple que cualquier presentación formal resulta superflua. Existen, a pesar de todo, importantes concepciones erróneas sobre el carácter fundamental del método y sobre los detalles de su uso. Estos errores están tan extendidos, y han influenciado tan profundamente el carácter de tantas especulaciones […]
[…] poner de relieve los puntos sobre los que son más comunes las confusiones, tales como el de la naturaleza de la fórmula dimensional, el número apropiado de unidades fundamentales, y la naturaleza de las constantes dimensionadas”. El uso de negritas es nuestro.
3 Traducción: “Todo físico sabe cómo realizar un análisis dimensional y cómo calcular las unidades de una magnitud dimensionalmente compleja, pero, de hecho, ninguna teoría ha justificado adecuadamente estas operaciones. Lo que es peor: los dos conceptos [dimensiones y unidades de las magnitudes físicas] se mezclan frecuentemente. Peor aún: con frecuencia se “definen” mediante referencias a operaciones de medida …
El Análisis dimensional constituye una rama establecida de los fundamentos físicos. Sin embargo, tiene más de colección dispersa de conceptos, teoremas y reglas que de sistema hipotético-deductivo. Se encuentra casi en el mismo estado que el cálculo operacional de HEAVISIDE antes de ser legitimado por la teoría de transformadas de Laplace. Tanto es así que el análisis dimensional ni tan siquiera aporta un análisis matemático de la propia noción de dimensión”.
4 Los conceptos primarios de la física exigen una catalogación propiamente lingüístico-filosófica y deben expresarse para su concreta elaboración mediante formulación matemática. De ahí que ofrezcan una doble naturaleza: filosófica (que con harta frecuencia se olvida) y matemática, que será la que le otorgue el valor de su aplicación en magnitudes, leyes, ecuaciones, fenómenos, problemas, etc.
5 Bunge, M. (1981).
6 Estos conceptos de cantidad, unidad, medida y magnitud son conceptos primiciales para la construcción de las teorías matemáticas básicas de la física. Son, así, conceptos con relevancia intrínseca a los que no les afecta la idea, tan necesaria y útil en campos subsiguientes, de ‘por convenio’. Filosóficamente decimos que lo son ‘por sí mismos’, de suma claridad.
7 Un concepto puede expresarse, como manifestación de riqueza lingüística, mediante diversos términos. Hay que evitar la utilización de un único término para diferentes conceptos. Aquí, siguiendo a la rica Escuela Española de Análisis Dimensional, iniciada por Julio Palacios, se distingue perfecta y precisamente entre la clase -magnitud- y sus elementos -cantidades-. En la Naturaleza existen ‘cantidades de’ -por eso son los entes primiciales- una determinada ‘magnitud’.
9 En la teoría que se construye como fundamentos de física, medida es también concepto teórico. En las aplicaciones, tanto teóricas como experimentales e industriales, la medida es el resultado de un proceso de medición, en perfecta consonancia con el valor medido (VIM 2.10).
BIBLIOGRAFÍA BÁSICA
BRIDGMAN, P.W. (1922): Dimensional Analysis. Yale University Press, New York. AMS. (2ª ed. revisada, 1931). [Versión española de F.A. González Redondo (1990), con supervisión de F. González de Posada. Madrid: Grupo de Trabajo de Análisis Dimensional].
– – – (1936): The Nature of Physical Theory. Princeton University Press, New Jersey.
– – – (1952): The Nature of Some of our Physical Concepts. Philosophical Library, New York.
BUNGE, M. (1967a): Scientific Research. New York: Springer-Verlag [ed. castellana La investigación científica. Barcelona: Ariel. 1969. 2ª ed. corregida 1985. [Trad. Miguel A. Sacristán].
– – – (1967b): Foundations of Physics. New York: Springer-Verlag.
– – – (1971): “A Mathematical Theory of the Dimensions and Units of Physical Quantities”, en Bunge M. (ed.): Problems in the Foundations of Physics. Springer-Verlag, New York.
GONZÁLEZ DE POSADA, F. (1981): “Hacia una nueva fundamentación del Análisis Dimensional”. Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales, vol. 75, 969-991.
– – – (1984): “Los conceptos de métrica, longitud y magnitudes espaciales referenciales en Análisis Dimensional. (El espacio geométrico como prefísica). Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales, vol.78, 3º. 1984. (11 pág.).
– – – (1992): “Nuevos conceptos básicos en Teoría Dimensional: hipótesis magnitudinales, principios ecuacionales y leyes relacionales” en Anuario Científico 1991 del Grupo de Trabajo de Análisis Dimensional. Universidad Politécnica de Madrid. I.S.B.N: 84-87596-09-06, 11-13.
– – – (1994): Breviario de Teoría Dimensional. ISBN: 84-605-0968-0. Fundación General de la Universidad Politécnica de Madrid.
– – – (2002): “Fundamentals of Dimensional Theory”, con la colaboración de F.A. González Redondo. En Journal of New Energy (USA). Vol. 6, No 4, 45-61.
GONZÁLEZ REDONDO, F.A. (1993): El Análisis Dimensional en la obra de Mario Bunge. Tesis doctoral en Filosofía de la Ciencia dirigida por F. González de Posada. Facultad de Filosofía. Universidad Complutense de Madrid.
– – – (2000): Historia del Análisis Dimensional. Tesis doctoral en Matemáticas dirigida por F. González de Posada. Universidad Politécnica de Madrid.
PALACIOS, J. (1941): Magnitudes y unidades electromagnéticas. Madrid: Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales, 35, 148-179.
– – – (1953): El lenguaje de la Física y su peculiar filosofía. Madrid: Real Academia Española.
– – – (1956): Análisis Dimensional. Madrid: Espasa-Calpe. [Edición en francés: L’Analyse Dimensionnelle. París: Gauthier Villars, 1960. Edición en inglés: Dimensional Analysis. New York-London: MacMillan, 1964. 2ª edición en español: Análisis Dimensional. Madrid: Espasa-Calpe, 1964].
– – – (1960): Relatividad. Nueva Teoría. Madrid: Espasa-Calpe.








Comentarios