El Problema de la G ‘grande’ de Newton: medidas cuánticas para su posible solución

Miguel A. Martin-Delgado ^(1,2)
(1) Departamento de Física Teórica, Facultad de Ciencias Físicas. Univ. Complutense, Madrid, España.
 ⁽²⁾ mardel@ucm.es. +34 913944526

RESUMEN: Este artículo tiene como objetivo explicar cómo con coherencia cuántica se puede medir G en el contexto de la segunda revolución de las tecnologías cuánticas, y, además, se explicarán otras nociones de interés relacionadas. La fuerza de la gravedad es la interacción fundamental conocida con mayor antigüedad. Sin embargo, su constante fundamental G de Newton es una de las peor medidas según los valores del CODATA 2014, con una incertidumbre relativa de 4,7 x 10^-5 frente a 2,3 x 10^-10 de la constante de estructura fina electromagnética a_EM. Estas imprecisiones tan grandes representan un gran inconveniente en metrología que ha hecho necesario la introducción del llamado ‘kilogramo cuántico’ en el  Sistema Internacional de unidades recientemente revisado. La posibilidad de que todavía existan errores sistemáticos desconocidos en las mediciones tradicionales basadas en métodos clásicos hace que sea importante medir G con métodos independientes, como los cuánticos.

Palabras clave: Cuántica, medidas cuánticas, gravedad, constantes físicas

ABSTRACT: This article aims to explain how quantum coherence can measure G in the context of the second revolution of quantum technologies, and, in addition, other related notions of interest will be explained. The force of gravity is the fundamental interaction known with greater antiquity. However, its fundamental constant G of Newton is one of the worst measures according to the values ​​of CODATA 2014, with a relative uncertainty of 4,7 x 10^-5 versus 2,3 x 10^-10 of the electromagnetic fine structure constant a_EM. These large inaccuracies represent a major inconvenience in metrology that has made it necessary to introduce the so-called ‘quantum kilogram’ into the recently revised International System of Units. The possibility that there are still unknown systematic errors in traditional measurements based on classical methods makes it important to measure G with independent methods, such as quantum ones.

Keywords: Quantum, quantum technologies, quantum metrology, gravity, physical constants,…

1. INTRODUCCIÓN

La constante G de la gravitación universal de Newton es la más antigua de las constantes fundamentales de la naturaleza, y, sin embargo, es la medida con peor precisión, según los valores del CODATA 2014, con una incertidumbre relativa de 4,7 x 10^-5, frente a 2,3 x 10^-10 de la constante de estructura fina electromagnética α_EM.

Mejorar la precisión con la que conocemos G no sólo tiene un interés metrológico puro, sino que también es importante debido al papel clave que G tiene en las teorías de la gravitación, la cosmología, la física de partículas y la astrofísica, y en los modelos geofísicos. Si bien, hay muchos cálculos espaciales, astronómicos, cosmológicos etc. que no se ven afectados por el valor de G ya que el valor que interviene es la combinación G M, donde M es la masa fuente.

La medición de un valor más preciso de G beneficiará muchos campos de la física y la metrología, como la comprensión del efecto Casimir, la mejora de las constantes de resorte que se utilizan para calibrar microscopía de fuerza atómica y la comprensión de las fuerzas intermoleculares en el ADN [1]. Un valor preciso de G también podría utilizarse para sondear las teorías propuestas que unifican la gravedad con la electrodinámica cuántica.

2. EL PROBLEMA DE LA G ‘GRANDE’

Más específicamente, el problema de la G grande (PGG) tiene dos aspectos fundamentales que permanecen como problemas abiertos:

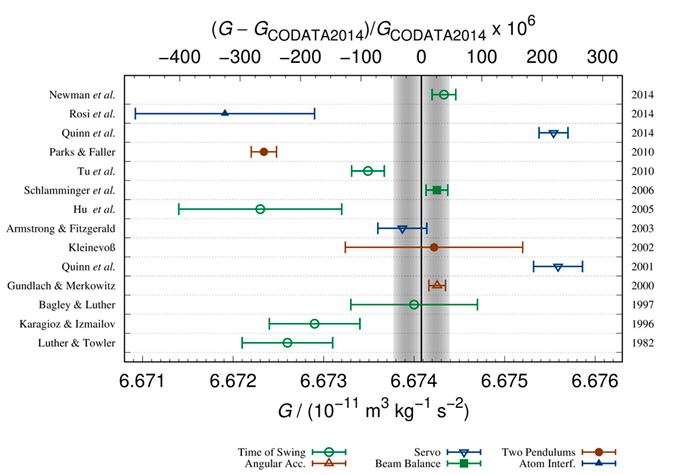
PGG-I: los diferentes experimentos clásicos de la medida de G dan resultados que no convergen a un valor fijo de G, después de muchos años de medidas independientes (ver Fig.1).

Estas mediciones divergentes lo son aún teniendo en cuenta sus márgenes de error. Cuanto mejor se trata de medir G, con mayor precisión, más divergentes se vuelven los resultados. Esta situación es bastante llamativa en metrología, y frustrante [1].

Este desacuerdo cuestiona nuestra capacidad de medir fuerzas pequeñas a escala de laboratorio. También plantea la cuestión de si la ley de fuerza newtoniana es una descripción completa de la gravedad a estas distancias. Sería una pena si una física nueva estuviera manifestándose ante nuestros ojos en los valores de dispersión de la Fig.1 y no la comprendemos del todo, porque consideramos que la medición de la constante G no tiene importancia. Es un problema de gran interés científico ver si podemos medir esta constante con incertidumbres por debajo de 10^-5. Existe una pequeña posibilidad de que estas discrepancias se deban a que realmente no conocemos del todo la teoría de la gravitación. Si fuera así, estas divergencias serían una señal de una posible nueva física.

Sin embargo, la hipótesis más probable es que las discrepancias se deban a errores sistemáticos que se han colado en las medidas del BIPM (Bureau International des Poids et Measures). Se decidió hace unos años que estas pruebas se llevaran a cabo de nuevo con el mismo equipo, pero en una instalación diferente y con un equipo diferente. Los investigadores del NIST asumieron el desafío y actualmente se están preparando para repetir el experimento BIPM utilizando el aparato original, con algunas actualizaciones.

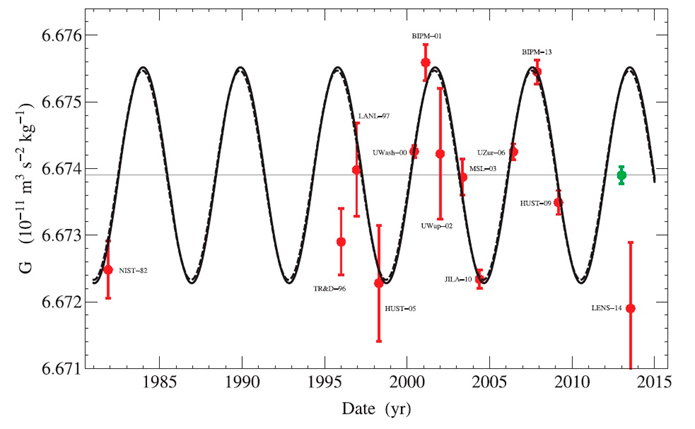
PGG-II: existe una anomalía en la determinación experimental de G que varía quasi-periódicamente con el tiempo (calendario) (ver Fig.2).

Recientemente, varios grupos científicos han encontrado que los valores medidos de G oscilan en el tiempo como una onda sinusoidal con un período de 5,9 años [2]. De nuevo, esto abre interrogantes sobre el origen de esta oscilación. Esta vez no se cree que sea algo intrínseco a la constante G. Se piensa que es más probable que algo más esté afectando las mediciones.

Un indicio en este sentido es la observación de que la citada oscilación se correlaciona casi perfectamente con el período oscilante de 5,9 años de la tasa de rotación de la Tierra, según se ha determinado por las medidas recientes de la Longitud del Día (LOD=Length of Day). Lo interesante de esta discrepancia es que es predecible, al contrario de la PGG-I.

LOD se refiere al exceso de la duración del día (período observado de rotación de la Tierra) relativo a una unidad estándar y se calcula tomando la diferencia entre el tiempo atómico (TAI) y el tiempo universal (UT1) dividido por la unidad estándar antes mencionada de 86400 SI s.

Una posible explicación podría implicar corrientes circulantes en el núcleo de la Tierra. Las corrientes cambiantes pueden modificar la inercia rotacional de la Tierra, afectando al LOD, y podrían estar acompañadas por variaciones de densidad, afectando así a G.

A pesar de la estrecha correlación entre LOD y G, no está claro que sea suficiente para explicar la oscilación temporal en G. De hecho, las observaciones experimentales indican que la variación porcentual máxima de la LOD es del orden de 10^-9, que implica un cambio en G de sólo 10^-5 de su magnitud. Esto resulta insuficiente para explicar una variación de 10^-4 % en G. Como esto significaría que las variaciones de LOD no pueden causar las variaciones observadas de G, los investigadores suponen que ambas variaciones son causadas por movimientos cambiantes en el núcleo de la Tierra, o tal vez por algún otro proceso geofísico. En todo caso, su origen permanece como un problema abierto en la medición de G grande.

3. EXPERIMENTOS CLÁSICOS

Las mediciones de la constante G grande de Newton se han realizado tradicionalmente por el método de la balanza de torsión y sus variantes [3]. De hecho, este método es el propuesto originalmente por Cavendish en 1798 [4] en su famoso experimento para ‘pesar la Tierra’. Cavendish se apoyó en la balanza del reverendo John Mitchell, pero la perfeccionó tanto que la rehízo por completo. J. Mitchell también quería pesar la Tierra, y no solo eso, también la luz. De ahí llegó a plantear el concepto de agujero negro que denominó ‘estrellas oscuras’ [5].

También las nuevas mediciones propuestas para resolver el PGG-I ilustrado en la Fig.1 están basadas en balanzas de torsión, aunque con muchos refinamientos, como introduciendo cuatro masas prueba de cobre en forma de cilindro (además de las masas de referencia M externas) [1]. La complejidad de los nuevos experimentos requieren de una máquina de medidas de coordenadas de los distintos elementos de la balanza.

La balanza de torsión merece un comentario histórico por su relación con el sistema de unidades de medida. ¿Qué midió Cavendish y porqué es importante? [6] Cavendish no midió G pues ésta no era posible introducidirla en 1798. Newton planteó la Ley de Gravitación Universal como una proporcionalidad,

F α M m/R²,                          (1)

no como una igualdad. El sistema de unidades actual no existía en época de Newton. El sistema de unidades proviene de los físicos y matemáticos franceses en el s. XIX. El primero en introducir constantes físicas para formular leyes en términos de igualdades fue J.B. Fourier en 1822 en su tratado analítico del calor [7]. De esta manera se podían plantear ecuaciones diferenciales y resolverlas más sistemáticamente que con las incómodas expresiones basadas en proporcionalidades.

En este punto, surge otra pregunta: ¿Quién introdujo la G? No fue Newton, ni Mitchell, y Cavendish tampoco. La primera vez que aparece una ecuación, i.e., igualdad en vez de proporcionalidad, es en la 4ª edición de “Cours élémentaire de Physique” (Paris, 1844), de Nicolás Deguin. Aunque éste hecho debe ser posterior pues una traducción de la segunda edición de ésta obra ya la introduce: Curso elemental de Física (Madrid, 1841) de Venancio González Valledor, catedrático de Física en los Estudios de San Isidro en Madrid. Si bien hay que hacer notar que no se usa el símbolo G, sino f, y no se le da ningún valor numérico [6]. El símbolo f lo utiliza por primera vez S. D. Poisson en “Traité de Mécanique” (1811) al escribir la ley de la gravitación como una igualdad [8].

El valor numérico de f aparece más tarde, en 1873, en un trabajo presentado a la Academia de Ciencias de Paris: ‘Détermination nouvelle de la constante de l’attraction et de la densité moyenne de la Terre’ por A. Cornu and J. Baille [9]. Ésta es realmente la primera determinación experimental del valor de G [8].

Finalmente, aparece el símbolo G en un trabajo conocido de J.H. Poynting de 1892. Sin embargo, el primer uso de G es incluso anterior, a tenor de lo que el propio Poynting hace notar en su artículo. Siguiendo sus anotaciones [6], la primera aparición conocida de G se debe a Arthur Köning y Franz Richarz en la revista de la Real Academia en 1884 y en la revista Nature de 1885 [10]. El propio Poynting volvió a determinar experimentalmente el valor de la masa de la Tierra en la universidad de Birmingham en 1890.

En definitiva, Cavendish midió la densidad media de la Tierra tratando de contribuir a solucionar un problema de actualidad entoces: la composición y forma de la Tierra. El concepto de G como constante de la gravitación universal era prematuro. Su introducciónen la ley de la gtravitación tiene carácter dimensional: establecer la homogeneidad de las unidades físicas en las mismas unidades en ambos miembros de una igualdad.

4. EXPERIMENTOS CUÁNTICOS

En estas circunstancias, y sospechando que el origen de los problemas PGG son de tipo errores sistemáticos, está justificado el buscar métodos alternativos y de naturaleza completamente distinta a los métodos tradicionales de la balanza de torsión.

Las medidas cuánticas de la constante G grande [11]  son precisamente un claro ejemplo de técnica innovadora en este tipo de problema donde sólo un método ha  sido el dominante hasta hace poco: los basados en la balanza de torsión.

El método cuántico de los Átomos Fríos en Gravedad (AFG) [11]  consta de 2 pasos:

Paso 1: medida de la constante g pequeña: valor de la gravedad local terrestre.

Paso 2: medida de la constante G grande.

Una observación importante (ver Conclusiones) es que es un método indirecto de medición para la G grande de Newton, al contrario de la balanza de Cavendish que es un método directo de medir G.

Es una técnica basada en interferometría atómica con átomos ultrafríos. Con ella, se hace uso de la naturaleza cuántica de los átomos a temperaturas cercanas al cero absoluto, para obtener una medida precisa de la aceleración de la gravedad. La técnica consiste en voltear átomos fríos verticalmente, arriba y abajo, de forma repetida. Esto sirve para sondear la gravedad terrestre con una nube de átomos de rubidio Rb en caída libre, como en el famoso experimento de Galileo [12]  que tanto utilizó Einstein en su teoría general de la relatividad [13]. Con esto se consigue medir la fuerza de la gravedad entre un átomo de Rb y una masa de referencia de 516 kg. El resultado es una medida de G con una incertidumbre relativa del 0,015 % (ver Fig.1).

A continuación describimos cada paso más en detalle:

Paso 1: Se prepara una nube de átomos en dos estados cuánticos distintos, A y B. Usando pulsos de luz de una forma apropiada, se puede inducir una transición de un estado A al B con una cierta probabilidad. Debido a la coherencia cuántica, cuando los átomos no son observados, pueden estar en una superposición de estados A y B con igual probabilidad 50 %. Además de inducir la transición, el pulso de luz comunica verticalmente un impulso lineal a los átomos en el estado B de modo que tienen más velocidad que los átomos en el estado A. La fracción relativa de átomos en los estados A y B varía con el tiempo, y su tasa de variación depende del producto del momento (diferencia) y la distancia vertical recorrida: Δp Δz.

Los átomos en el estado B recorren más altura que los A debido a su mayor velocidad, en presencia de la aceleración de la gravedad terrestre g. Entonces, la tasa de variación es función de g. Al caer la nube atómica al punto de lanzamiento, se mide la razón de átomos A a B y se extrae el valor de g [14].

Paso 2: Conocida g, podemos medir el valor de G mediante una masa de referencia M. Para simplificar el razonamiento, supondremos que M es puntual y que g también se ha medido en un punto fijo. Primero se dispone la masa de referencia una distancia z por encima del interferómetro y la g resultante tras la técnica del paso 1 es:

g_a = –g + G (M/z²)                   (2)

Después, se repite la medida poniendo la masa de referencia una distancia z por debajo, ahora:

g_b = –g – G (M/z²)                    (3)

De aquí obtenemos, de forma indirecta, la medida de G:

G = (g_a – g_b) z²/(2M)                          (4)

5. RESULTADOS Y DISCUSIÓN

El método cuántico AFG descrito anteriormente está simplificado en dos aspectos importantes: uno teórico y otro experimental.

En cuanto al aspecto teórico, la realidad es que la masa de referencia M no es puntual pues se trata de un objeto extenso con forma de cilindro y 516 kg de masa.  Y la medida de la g local no se realiza en un solo punto, sino a lo largo de una trayectoria. Todo esto se puede tener en cuenta con un análisis teórico más preciso que solo involucra unos cálculos más complicados.

Más importante resulta el aspecto de las interferencias experimentales: g cambia con el tiempo debido a las fuerzas de marea producidas por el Sol y la Luna, a las variaciones de la presión del aire y el movimiento de las masas en las cercanías del experimento (como en los métodos basados en la balanza de torsión).

Para resolver este problema de la variación de g con el tiempo, un equipo de tipo AFG tiene que medir g_a y g_b simultáneamente. Esto se consigue disponiendo dos interferómetros atómicos uno encima de otro. Se introducen dos masas de referencia M entre ambos interferómetros y se mide la diferencia entre g_a y g_b resultando ser independiente del tiempo, aunque dependiente de variaciones espaciales (porque las medidas se toman en sitios distintos). Para eliminar éstas, se vuelve a repetir el experimento con las masas M una por debajo del interferómetro más bajo, y la otra M por encima del más alto. Ahora la diferencia es independiente de la variación espacial de g. El valor estimado de G se obtiene promediando 100 medidas conjuntas de este tipo. El resultado es G = (6,67191 ± 0,00099) × 10^-11 m³ kg^-1 s^-2. La incertidumbre relativa de la medición es 0,015%. Podemos ver este resultado en la Fig.1 (parte superior izquierda). Todavía queda fuera de la zona vertical sombreada del valor recomendado más reciente para G según se observa en la Fig.1 para el PGG-I, y también es discrepante con el valor medio debido al PGG-II como se observa en la Fig.2 (ver Conclusiones).

Los métodos cuánticos como el AFG tienen ventajas e inconvenientes respecto a los métodos tradicionales de torsión. Una de las grandes ventajas de los métodos clásicos es que miden g en una dirección perpendicular a la vertical, con lo que se evitan errores sistemáticos causados por los cambios con el tiempo en g que aparecen en el AFG. Pero para captar la pequeñísima señal gravitatoria, el propio laboratorio tiene que ser mecánicamente estable, con un bajo nivel de vibración e inclinación del suelo, y con la temperatura de su aparato estabilizada a unas pocas milésimas de grado Celsius.

Por el contrario, el método AFG tiene la ventaja de que el átomo no requiere una conexión física al laboratorio y, por lo tanto, no está sesgado por las fuerzas dispersivas que tal conexión introduce en la medición. Recordemos que en la balanza de torsión se usan dos tipos de masas diferentes. Una masa m de prueba que está sujeta al péndulo de torsión, y una masa M más grande de referencia. Ambas por duplicado.

6. CONCLUSIONES Y PERSPECTIVAS

El llamado problema de la G grande de Newton (PGG) se ha vuelto muy desconcertante tras más de treinta años de toma de medidas por métodos tradicionales (clásicos): los valores medidos de G no parecen converger a ningún valor, y lo que es peor aún, la convergencia empeora con cada nuevo valor añadido a la lista de mediciones.

Aunque detrás de estas discrepancias podría encontrarse efectos relacionados con nuevos aspectos de la gravitación no conocidos anteriormente, sin embargo existen otros test experimentales que descartan modificaciones de la teoría de la gravitación de Einstein. Por ejemplo, se han usado medidas astronómicas con el Green Bank Telescope (GBT) de la National Science Foundation (NSF) en Virginia Occidental y su Observatorio Arecibo en Puerto Rico. El estudio se llevó a cabo durante 21 años para medir con precisión el ‘latido’ constante de un pulsar conocido como PSR J1713 +0747. Esta minuciosa investigación produjo la mejor restricción de la constante gravitacional medida fuera de nuestro Sistema Solar [15]. Esto apuntaría a errores sistemáticos detrás del PGG y a la necesidad de mejoras en metrología.

Con esta tendencia de resultados aislados que no resuelven el PGG, recientemente se ha propuesto aunar esfuerzos formando un consorcio internacional para enfrentarse al problema [1]. Una idea básica propuesta es la de intercambiar aparatos entre distintos laboratorios y repetir las mediciones con el fin de detectar posibles errores sistemáticos. La única manera de conseguir confianza y reducir errores sistemáticos es medir la misma constante usando una serie de métodos diferentes. Esto es cierto en la medición no sólo de una constante fundamental de la naturaleza como G, sino de cualquier otro observable.

El experimento cuántico AFG es muy diferente de todas las demás mediciones [11], y el tamaño de la incertidumbre alcanzada, aunque todavía algo grande, se aproxima a los obtenidos usando balanzas de torsión. En los últimos 6 años, este equipo ha reducido la incertidumbre de su experimento por un factor de 10 en comparación con un resultado preliminar publicado en 2008 [16]. Como complemento a los esfuerzos del BIPM para resolver el PGG con métodos clásicos, sería muy conveniente aumentar el número de medidas cuánticas realizadas por un mayor número de laboratorios y ver como se distribuyen en la Fig.1. Si sucede que las medidas cuánticas sí convergen a un mismo valor sería un indicio claro de que los métodos clásicos sufren de algún error sistemático desconocido.

Como se hizo notar en el apartado 4, es de resaltar que los métodos cuánticos como el AFG utilizan la g-pequeña para obtener la G de forma indirecta. Podríamos pensar si sería posible utilizar un método directo de medir cuánticamente la G grande. Pero fijémonos que esto implicaría la primera medida experimental cuántica de la gravitación, y esto está todavía muy lejos de conseguirse.

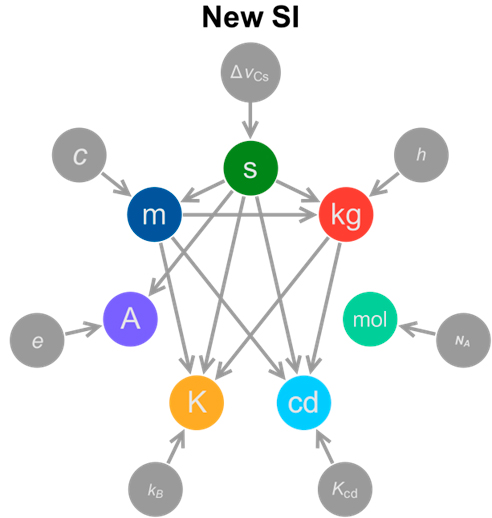
El nuevo Sistema Internacional (SI) ha sido revisado y ha entrado en vigor el 20 de mayo de 2019. Su principal cambio consiste en la definición de las unidades físicas en términos de las constantes fundamentales de la naturaleza (ver Fig.3). Curiosamente, no aparece la G entre ellas. De hecho, el kilogramo como unidad de masa está definido a través de la constante h de Planck: el llamado `kilogramo cuántico’, utilizando el efecto Hall y el efecto Josephson para ello, junto con la balanza de Kibble [17]. Este hecho es de nuevo indicativo de que el PGG sigue abierto en metrología. No se puede dar una realización gravitacional del kilogramo a través de la G pues está determinada con poca precisión y, en cambio, se usa otro camino que involucra la constante h de Planck que está mucho mejor medida.

5. REFERENCIAS

[1] http://pml.nist.gov/bigg

[2] J. D. Anderson, G. Schubert, V. Trimble and M. R. Feldman, Europhysics Letters, 110 (2015) 1.

[3] T. Quinn, Nature 408, (2000) 919.

[4] H. Cavendish, ‘Experiments to determine the Density of the Earth’. Philosophical Transactions of the Royal Society of London, (part II) 88 (1798) 469-526.

[5] J. Mitchell. Philosophical Transactions of the Royal Society of London. 74: 35–57. 1784.

[6] A. Moreno; “Weighing the Earth: a Newtonian Test and the Origin of an Anachronism”. Science & Education 10(6):515-543,  (2001).

[7] Jean Baptiste Fourier, ‘Théorie analytique de la Chaleur’, 1822.

[8] A. Moreno; “De fµmm´/d² a f = G mm´/d²: Aclaraciones sobre una historia mal contada”. Enseñanza e Historia de las Ciencias y de las Técnicas: Orientaciones, Metodologías y Perspectivas, Barcelona, 2014, SEHCYT, 17-25.

9] A. Cornu and J. Baille (Comptes Rendus, 1873, 76(15), 954–958).

[10] A. König, F. Richarz. `Eine neue Methode zur Bestimmung der Gravitationsconstante´. Sitzungsberichte der Kijniglich Preussischen
Akademie von Wissenschaft zu Berlin, 1884 : 1203-1205. Nature, XXXI, (1885), 260, 484.

[11] G. Rosi, F. Sorrentino, L. Cacciapuoti, M. Prevedelli and G.M. Tino, Nature 510, (2014) 518.

[12] E. Giusti, “Galileo’s De motu antiquiora,” Nuncius 13, no. 2 (1998) 427.

[13] A. Einstein, Sitzungsberichte der Preussischen Akademie der Wissenschaften zu Berlin (1915), 844.

[14] M. Kasevich and S. Chu,  Phys. Rev. Lett. 67, (1991) 181.

[15] W. W. Zhu, I. H. Stairs, P. B. Demorest, D. J. Nice, J. A. Ellis, S. M. Ransom, Z. Arzoumanian, K. Crowter, T. Dolch, R. D. Ferdman, E. Fonseca, M. E. Gonzalez, G. Jones, M. L. Jones, M. T. Lam, L. Levin, M. A. McLaughlin, T. Pennucci, K. Stovall, J. Swiggum, ApJ 809, (2015 ) 41.

 [16] G. Lamporesi, A. Bertoldi, L. Cacciapuoti, M. Prevedelli, and G. M. Tino Phys. Rev. Lett. 100, (2008) 050801.

[17] M.A. Martin-Delgado. “The New SI and the Fundamental Constants of Nature” preprint 2019.

6. AGRADECIMIENTOS 

Mi agradecimiento a José Ángel Robles Carbonell por su continuo apoyo para presentar este artículo como una ponencia en el 6º Congreso Español de Metrología (San Fernando de Cádiz, 2017). Mi agradecimiento a Antonio Moreno por conversaciones sobre la historia de la medición de G y a Alberto Galindo por su invitación a una sesión científica en el ciclo ‘Ciencia para Todos’ de la Real Academia de Ciencias Exactas, Físicas y Naturales de España (Madrid, 2018). Se agradece el apoyo financiero de los proyectos MINECO FIS2015-67411, consorcio CAM de investigación  QUITEMAD-CM, Grant No.S2018/TCS-4342., proyecto Explora FIS2017-91460-EXP y U.S. Army Research Office via Grant No. W911N F-14-1-0103.