Alicia Pons
Instituto de Óptica “Daza de Valdés”, Agencia Estatal CSIC (IO-CSIC),
C/. Serrano 144, 28006, Madrid, España
alicia.pons@csic.es.
Resumen
La Fotometría clásica se basa en el uso de fuentes de incandescencia de filamento de tungsteno y de detectores con filtro V(λ) como patrones de transferencia en la calibración de las diferentes magnitudes fotométricas, y se estableció mucho antes de que las fuentes de luz de estado sólido (SSL) estuviesen disponibles para su uso en iluminación general. En gran parte debido a las regulaciones políticas, las lámparas de incandescencia casi han desaparecido del mercado. Debido a esto, también está a punto de desaparecer el conocimiento de producir lámparas patrón de calidad basadas en incandescencia. Esto, a su vez, significa que la trazabilidad metrológica actual basada en la fotometría clásica necesita ser reemplazada por otras soluciones en un futuro próximo. Es de la máxima prioridad encontrar alternativas a las lámparas de incandescencia y las basadas en LEDs parecen ser buenos candidatos.
Palabras clave: iluminantes patrón basados en LEDs, detectores con filtro V(λ), error de desajuste espectral, detectores de eficiencia cuántica predecible
Abstract
The classical photometric system relies heavily on tungsten filament standard lamps and V(λ) filtered detectors as transfer standards in the determination of photometric quantities; and was established long before SSL products became available for general lighting. Largely due to political regulations, consumer incandescent lamps have almost disappeared from the market. Because of this, also the knowledge of producing incandescent standard lamps is about to disappear. This, in turn, means that the present metrological traceability in classical photometry simply needs to be replaced by other solutions in the near future. It is of the highest priority to find alternatives to incandescent standard lamps, and LED-based standards are good candidates.
Key words: LEDs based standard iluminants, V(λ) filtered detectors, mismatch factor, predictable quantum efficient detector
1.- Introducción
La necesidad de la fotometría basada en LEDs surge de las tendencias claramente identificadas en la eliminación gradual de las lámparas de incandescencia y el creciente mercado de soluciones basadas en iluminación LED. Los usuarios de instrumentos fotométricos ya no realizan medidas de iluminación incandescente, sino principalmente de iluminación LED.
Sin embargo, todos los equipos fotométricos (luminancímetros, fotómetros o luxómetos) se calibran todavía usando lámparas patrones de incandescencia con distribuciones espectrales que simulen el iluminante A de la CIE [1], que describe iluminación incandescente con temperatura de color correlacionada de 2856 K. Estos instrumentos son posteriormente usados para probar el rendimiento de nuevos productos de estado sólido que llegan al mercado, como lámparas y luminarias, o en mediciones de campo para inspeccionar la calidad de la iluminación en oficinas, fábricas, aeropuertos y otros lugares públicos, donde la seguridad y el confort son de gran importancia.
El punto principal es que muchas aplicaciones de iluminación que antes usaban iluminación incandescente ya se han convertido para usar iluminación LED. En Europa, la tendencia hacia una iluminación de estado sólido, que ahorra energía, se ha acelerado gracias a la normativa y directivas de la UE [2,3,4], que abordan diversos tipos de fuentes de luz según su consumo de energía y otros aspectos ambientales, como el contenido de mercurio. Además de estas regulaciones, la futura penetración en el mercado de los productos LED dependerá de los costos de por vida y, por lo tanto, del rendimiento y la eficiencia energética de los productos LED en comparación con los productos de iluminación tradicionales que todavía están disponibles en el mercado; información que requiere una infraestructura metrológica adecuada para su correcta valoración.
Por otro lado, los laboratorios de calibración primarios se enfrentan a una situación en la que las lámparas patrones de incandescencia, usadas todavía en la actualidad como fuentes de calibración en fotometría, no estarán disponibles en el futuro. Como resultado de la eliminación progresiva de las lámparas de incandescencia, también se perderá el conocimiento y la capacidad para fabricar lámparas de la más alta calidad para la realización, difusión y mantenimiento de las magnitudes fotométricas. Algunas de las vigentes intercomparaciones del Comité Consultivo para la Fotometria y la Radiometría (CCPR) del CIPM, como la CCPR-K1 de Irradiancia espectral, la CCPR-K3 de Intensidad Luminosa y la CCPR-K4 de Flujo Luminoso, ya están sufriendo esta situación. Los participantes se enfrentan a problemas para encontrar lámparas de filamento de tungsteno adecuadas para la comparación, bien porque los tipos de lámparas utilizados en el pasado no están disponibles, o porque la calidad de los bulbos de última generación es cada vez peor. Esta situación obliga a los Laboratorios Nacionales a intentar mantener las lámparas antiguas el mayor tiempo posible.
Es urgente, por tanto, establecer un nuevo sistema fotométrico basado en una tecnología que ya está disponible y que será, presumiblemente en el futuro ampliamente utilizada. El Instituto de Óptica de la Agencia Estatal CSIC participa, dentro de un consorcio de institutos nacionales de metrología de países europeos, en el proyecto EMPIR 15SIB07 PhotoLED, que tiene el objetivo de desarrollar y validar la base para un nuevo sistema fotométrico basado en LEDs, encuadrado en tres grandes bloques: desarrollo de iluminantes y lámparas patrones basadas en LED, desarrollo de nuevos métodos de medida fotométrica y la reducción de incertidumbres en la medida de la eficacia luminosa de fuentes de estado sólido.
En este artículo se presenta una revisión de la situación actual de desarrollo de los objetivos principales que dicho proyecto pretende cubrir.
2.-Desarrollo de Iluminantes patrón basados en LED para fotometría y colorimetría.
En la actualidad sólo hay dos iluminantes patrón utilizados en fotometría y colorimetría: el Iluminante A, que describe la típica iluminación de incandescencia, y el Iluminante D65, que describe la luz del día [1]. Además de estos dos iluminantes patrón, la CIE define varios iluminantes más, que describen otros tipos de fuentes de luz, como los tubos fluorescentes y las lámparas de descarga que se utilizan en cálculos colorimétricos [5]. Sin embargo, hasta ahora no se habían definido iluminantes basados en LED.
El calibrado de un fotómetro, ya sea con respecto a un fotómetro de referencia o una fuente patrón de intensidad luminosa, se realiza siempre usando como fuente de radiación una lámpara de incandescencia que simule el Iluminante A de la CIE. Cuando se utiliza el fotómetro calibrado para medir fuentes de radiación con distribuciones espectrales diferentes de la de la fuente de calibración (por ejemplo, cuando se usa para medir iluminación LED); y, dado que en general la responsividad espectral de los fotómetros difiere de la curva V(λ) definida por la CIE, se produce un error que hace aumentar la incertidumbre de las magnitudes medidas con el fotómetro calibrado.
Este error se puede evaluar a través del factor de corrección de desajuste espectral (mismatch factor) definido como:
\({ ccfS }{ t }\left( \lambda \right) =\frac { \int { { S }{ t }\left( \lambda \right) { V }\left( \lambda \right) } d\lambda }{ \int { { { S }{ cal }\left( \lambda \right) { V }\left( \lambda \right) }d\lambda } } .\frac { \int { { { S }{ cal }\left( \lambda \right) { S }{ rel }\left( \lambda \right) }d\lambda } }{ \int { { { S }{ t }\left( \lambda \right) { S }_{ rel }\left( \lambda \right) }d\lambda } }\) (1)
donde Scal(λ) es la distribución espectral del iluminante para el que se ha calibrado previamente el fotómetro (en general iluminante A) , St(λ) es la distribución espectral relativa de la fuente que se quiere medir (LED en este caso), srel(λ) es la responsividad espectral relativa del fotómetro y V(λ) es la eficiencia espectral luminosa definida por la CIE [6]. El factor de corrección tiene un valor unidad si el fotómetro tiene una responsividad espectral ideal, es decir si srel(λ)=V(λ) o si las distribuciones espectrales relativas de la fuente a medir y la fuente de calibración tienen la misma forma. Por el contrario, si los espectros de las fuentes son muy diferentes, el error por desajuste espectral puede llegar a ser muy grande. Evitar este error pasa por la determinación del factor de corrección, para lo cual es necesario conocer tanto la responsividad espectral relativa del detector como el espectro de la fuente a medir, magnitudes que no son habitualmente conocidas por muchos usuarios.
Para minimizar este problema, la CIE venía recomendando [7], para la medida de fuentes LED, el uso de fotómetros con buenas responsividades espectrales (f’1 < 3%) (factor de calidad que describe como de bien se aproxima la responsividad espectral del detector a la V(λ)) o el método de “sustitución estricta” en el que el LED a medir se compara con un patrón LED “que tenga el mismo color”.
Recientes estudios [8] han demostrado que es posible reducir drásticamente el error por desajuste espectral si se sustituye el Iluminante A, como fuente de calibración, por un iluminante LED; incluso en casos en que el espectro del LED a medir difiera considerablemente del iluminante LED, con lo que el método de comparación no puede considerarse “estricto”. En concreto, demuestran que es posible reducir en un factor tres el error debido al desajuste espectral, si en lugar de usar una lámpara de incandescencia como fuente de calibración, se usan dos fuentes basadas en LED (representando los espectros de LEDs blanco cálido y blanco frio).
Si a esto se añade el hecho de que las lámparas de incandescencia tienen un tiempo de vida mucho más limitado y son mecánicamente más frágiles que los LEDs, se entiende la ventaja potencial de definir nuevos iluminantes LED, es decir definir distribuciones espectrales que definan productos de estado sólido típicos.
Con este objetivo, en el proyecto se han analizado alrededor de 1500 (en concreto 1516) distribuciones espectrales relativas de LEDs blancos comerciales de diferentes tipos, fabricados ente 2009 y 2016 [9]. Las medidas se han realizado en varios laboratorios, incluyendo fabricantes de productos LED, laboratorios de ensayo e Institutos Nacionales de Metrologia (INM), miembros del consorcio. Entre las distribuciones espectrales estudiadas había todo tipo de diferentes tecnologías, aunque al final, y dado que la mayoría de ellas eran LEDs blancos del tipo de LED azul con fósforo, se consideró este tipo de LEDs como el más conveniente y como posible fuente de calibración, debido a su disponibilidad, diseño relativamente sencillo y buen comportamiento respecto al envejecimiento, en comparación con otras tecnologías de LED blanco.
Las distribuciones espectrales se agruparon en ocho categorías diferentes según su temperatura de color correlacionada (CCT) nominal, basadas en el estándar C78.377.2011 del American National Standards Institute (ANSI) [10]: 2700 K, 3000 K, 3500 K, 4000 K, 4500 K, 5000 K, 5700 K y 6500 K. A continuación, y con objeto de no favorecer ningún producto LED comercial específico, se aplicaron diferentes métodos de promediado y ajustes [11] para finalmente llegar a obtener las distribuciones espectrales que se muestran en la Figura 1 .

Cinco de estas distribuciones, las correspondientes a los valores nominales de CCT: 2700 K, 3000 K, 4000 K, 5000 K y 6500 K (representadas en la figura 1 con líneas sólidas), se han propuesto a la CIE para que las incluya en la nueva edición de la publicación CIE 15. Colorimetry y se espera sean finalmente adoptados por la CIE como iluminantes para colorimetría [12] .
Una vez seleccionadas estas cinco distribuciones, el siguiente paso es seleccionar un espectro LED de referencia, que minimice el error de desajuste espectral, y que potencialmente pueda complementar, o incluso reemplazar, el iluminante patrón A en el calibrado de fotómetros.
Para determinar que espectro produciría, en promedio, el menor error de desajuste espectral, se han calculado los diferentes factores de corrección con cada una de esas distribuciones espectrales, usando los datos de responsividad espectral de alrededor de 100 (en concreto 107) fotómetros comerciales diferentes. Estos datos representan fotómetros reales que se usan en medidas fotométricas en los INM participantes, laboratorios industriales y en medidas de campo. El factor \({ { f }_{ 1 }^{ \prime } } \) de estos fotómetros varía entre 0,5 % y 8,8 %, siendo el valor medio de 3,2 %.
El cálculo se ha realizado partiendo de la ecuación (1) y usando como Scal(λ) cada uno de los cinco espectros seleccionados; las 1516 distribuciones espectrales analizadas como St(λ) y las responsividades espectrales relativas de los 100 fotómetros, como srel(λ) (es decir 107×1516 combinaciones diferentes). Por comparación, todo el análisis se ha repetido usando el iluminante patrón A como Scal(λ).
El resultado de este amplio estudio [9] fue que, en general, todas y cada una de las cinco distribuciones espectrales seleccionadas producen, de media, errores de desajuste espectral menores que el que se produce al usar el iluminante A como fuente de calibración; siendo la distribución espectral que representa la categoría de 4000 K, la que produce el menor error de desajuste espectral.
Finalmente, se ha analizado el efecto que produciría usar fotómetros calibrados con los iluminantes LED elegidos, al realizar medidas de otras fuentes de luz, usadas tradicionalmente en iluminación (luz de día, fluorescentes y lámparas de descarga de alta presión). De nuevo el espectro representado por la categoría 4000 K es el que da lugar al menor error de desajuste espectral.
2.1.- Lámparas patrón basadas en LED
Partiendo del espectro LED obtenido y en la confianza de que finalmente sea adoptado por la CIE como iluminante patrón para complementar el iluminante A en el calibrado de fotómetros, el siguiente objetivo dentro del proyecto es el desarrollo de fuentes patrones de intensidad y flujo luminosos. En colaboración con fabricantes de productos LED, participantes del proyecto, se han desarrollado ya algunas fuentes candidatas a ser patrón, con distribuciones espectrales que se ajustan al espectro LED seleccionado. En los próximos meses estas lámparas van a ser caracterizadas y evaluadas en dos intercomparaciones, para demostrar su viabilidad como patrones y su posible aplicación en intercomparaciones internacionales de fotometría, en sustitución de las obsoletas lámparas patrón de incandescencia.
Una vez validadas, las lámparas patrón basadas en LED podrán ser usadas en el calibrado de la responsividad luminosa de iluminancimetros, asegurando así la reducción de errores de desajuste espectral para la mayoría de los tipos de fuente de luz modernas. Esto beneficiará especialmente aquellos que no pueden aplicar la corrección de desajuste espectral, ya sea por su desconocimiento o en mediciones de campo de luz mixta de diferentes tipos, como la luz de día y los LEDs.
3.- Detectores de transferencia para el mantenimiento y diseminación de magnitudes fotométricas
Las magnitudes fotométricas Xv, se pueden calcular de las correspondientes magnitudes radiométricas Xe,λ(λ), como:
\({ X }_{ v }={ K }_{ m }\int { { X }_{ e,\lambda }\left( \lambda \right) } V\left( \lambda \right) d\lambda \) (2)
donde Km = 683,002 lm W-1 es la eficacia luminosa espectral máxima para visión fotópica, λ es la longitud de onda en aire y V(λ) es la función de eficiencia luminosa definida por el CIE.
La transferencia de las magnitudes fotométricas, desde los INM a los laboratorios de ensayo, se lleva a cabo utilizando lámparas patrón o fotómetros de referencia [13]. Un típico fotómetro de referencia consiste en una apertura de precisión, un fotodiodo de Si (único o en configuración de trampa) y un filtro óptico para ajustar su responsividad espectral relativa, srel(λ) a la función V(λ). La iluminancia medida por él se puede calcular a partir de la expresión:
\({ E }_{ v }=\frac { { K }_{ m } }{ As\left( { \lambda }_{ 0 } \right) } { F }_{ r }i\) (3)
Donde i es la fotocorriente medida por el detector, A es el área de la apertura de precisión y s(λ0) es la responsividad espectral absoluta del detector a la longitud de onda de 555 nm. El factor F es el factor de corrección de desajuste espectral definido de la forma:
\({ F }_{ r }=\frac { \int { \phi _{ e,\lambda }\left( \lambda \right) { V }\left( \lambda \right) } d\lambda }{ \int { { \phi _{ e,\lambda }\left( \lambda \right) { { S }_{ rel } }\left( \lambda \right) }d\lambda } } \) (4)
Notar que en este caso el factor de corrección solo depende de la diferencia entre la V(λ) y la responsividad espectral relativa del fotómetro de referencia.
El filtro óptico que ajusta la responsividad del detector a la V(λ) es el punto más débil e impredecible de un fotómetro, debido a su inestabilidad a largo plazo, su sensibilidad a la humedad y la estructura de su transmitancia. Todo esto se traduce en una contribución importante en el balance final de incertidumbre en el calibrado de fotómetros de referencia.
Por otra parte, dado que la emisión espectral de los LEDs blancos se limita, en general, al intervalo espectral cubierto por la función V(λ) (es decir el visible); en principio, si la responsividad espectral relativa de la fuente y la responsividad espectral absoluta del fotómetro de referencia se conocen con exactitud, se puede prescindir del filtro V(λ) en la medida de la iluminancia de LEDs; realizando la ponderación fotométrica numéricamente, aplicando la ecuación (4).
En los últimos años [14, 15, 16] hemos asistido al desarrollo de un nuevo patrón primario para la medida de la potencia óptica, basado en fotodiodos de unión inducida en configuración de trampa que tienen una eficiencia cuántica cercana a la unidad. Son los detectores conocidos como detectores de eficiencia cuántica predecible (PQED), cuya responsividad espectral absoluta se puede predecir con una incertidumbre relativa menor que 0,01 % [17, 18].
Usando un detector de este tipo, se puede entonces determinar la iluminancia de una fuente con una incertidumbre menor a la que actualmente se consigue con el método tradicional usando detectores con filtrado V(λ). Por supuesto, este método solo se puede utilizar cuando el espectro de emisión de la fuente a medir esté limitado al intervalo de respuesta de los fotodiodos de silicio, lo que sin duda se cumple en el caso de los LEDs blancos.
Además de la ventaja mencionada de eliminar los problemas producidos por el filtro óptico, la principal ventaja de este método es que simplifica la cadena de trazabilidad en la realización de las unidades fotométricas, lo que se traslada en una más baja incertidumbre.
Este efecto es evidente si comparamos la cadena de trazabilidad del método tradicional de calibrado de un fotómetro de referencia, con la cadena de trazabilidad del método basado en un PQED (figura 2). Como el PQED es un patrón primario, no hay necesidad de su calibrado respecto al radiómetro criogénico. Además, como la responsividad del PQED es perfectamente conocida y no se usa el filtro V(λ), tampoco es necesario utilizar un espectrómetro de referencia para la determinación de la responsividad espectral.
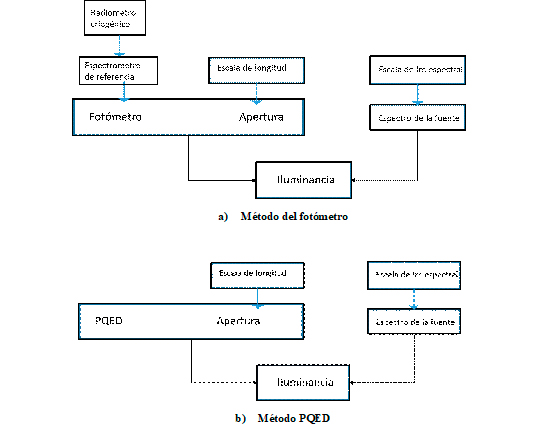
No obstante, los PQEDs sólo miden la luz que se propaga a lo largo del eje óptico, por lo que este método no se puede aplicar a medidas de iluminación LED general, en las que se suele utilizar un fotómetro equipado con un difusor. Por lo tanto, este método solo está reservado para aplicaciones donde se requiera la menor incertidumbre posible, como por ejemplo en el calibrado de iluminancimetros a nivel de laboratorio nacional.
En lugar de un PQED, es posible utilizar un detector con fotodiodos tradicionales en configuración de trampa; aunque en este caso el detector necesita calibrarse respecto al radiómetro criogénico y hay que medir o modelar su responsividad espectral. La incertidumbre final es algo mayor que la que se obtiene con el PQED, pero sigue teniendo la ventaja de no necesitar un filtro V(λ).
4.- Transferencia de la unidad de flujo luminoso
La mejora y desarrollo continuo de las fuentes de estado sólido (y en particular de los LEDs), pasa necesariamente por la posibilidad de medir de forma lo más exacta posible, su eficiencia energética; la cual se puede describir en términos de la eficacia luminosa, magnitud que se mide en lm por vatio (lm W-1) y que define la relación entre el flujo luminoso total y la potencia eléctrica consumida. En los laboratorios de ensayo, las medidas de flujo luminoso, incluidas las de las fuentes de estado sólido (LEDs), se realizan habitualmente mediante el uso de esferas integradoras, por comparación directa con lámparas patrones clásicas de filamento de tungsteno.
En este tipo de medidas, las principales fuentes de incertidumbre son debidas a las diferencias espectrales y angulares en la emisión de las fuentes y a la falta de homogeneidad de la reflectancia de la esfera.
Las nuevas lámparas patrones de flujo luminoso basadas en LED permitirán, como ya hemos visto, reducir los errores debidos a las diferencias espectrales. Sin embargo, los errores debidos a la no uniformidad de la reflectancia de la esfera, pueden verse incrementados por la diversidad (desde fuentes puntuales a omnidireccionales) de distribuciones espaciales de intensidad luminosa de los LEDs en comparación con la casi isotrópica distribución de las fuentes de incandescencia tradicionales. La corrección de esta no uniformidad espacial requiere conocer la distribución de reflectancia de la esfera [19, 20] así como la medida de la distribución angular relativa de intensidad del LED con un goniofotómetro, equipamiento que, dado el gran tamaño que se requiere de ellos, no suele estar disponible en los laboratorios de ensayo. La omisión de esta corrección en la medida en esferas integradoras puede llevar a un error en la media del orden del 2 % en la medida del flujo luminoso y, en consecuencia, en la determinación de su eficacia luminosa.
En relación con este tema, en el proyecto se ha puesto en marcha [21] un novedoso procedimiento basado en el uso de cámaras [22] para determinar la distribución angular de los productos de iluminación.
Los primeros resultados obtenidos con este método se han comparado con los obtenidos con el uso de goniofotómetros, obteniendo diferencias del orden de ± 0,15 %.
En los próximos meses, como se ha mencionado anteriormente, está prevista una intercomparación de medidas de flujo luminoso. Se pretende no solo validar las nuevas fuentes basadas en LED desarrolladas, sino también, aplicando el método mencionado basado en cámaras para la determinación de la no uniformidad de las esferas integradoras, verificar si es posible que los laboratorios de ensayo puedan obtener incertidumbres del orden del 1 % en la medida de la eficacia luminosa.
5.- Conclusiones
Este artículo recoge en forma resumida la situación actual de desarrollo de los objetivos de un proyecto de investigación EMPIR, enfocado en desarrollar y validar la base para un nuevo sistema fotométrico basado en LEDs. El nuevo sistema fotométrico tiene un gran potencial para dar un giro completo de la fotometría tal como la conocemos.
En el nuevo sistema de fotometría basado en LEDs, tanto el iluminante patrón A clásico, que corresponde a las lámparas patrón de filamento de tungsteno utilizadas para desarrollar los patrones de intensidad luminosa y flujo luminoso, como los fotómetros de referencia con filtro V(λ), que se usan tradicionalmente en los INM para el calibrado de las diferentes magnitudes fotométricas, serán reemplazados por iluminantes y lámparas patrón basadas en LED, así como nuevos fotómetros de referencia sin filtrado V(λ). Los nuevos fotómetros proporcionarán la capacidad de medir la iluminancia de las nuevas fuentes patrón con una incertidumbre tan baja como el 0,2 % (k = 2) en un INM, Este valor permitirá a su vez, en combinación con el nuevo método basado en cámaras para la determinación de la no uniformidad de esferas integradoras, alcanzar el objetivo de medir la eficacia luminosa de los productos de estado sólido en los laboratorios de ensayo, con una incertidumbre del 1 % (k = 2).
6.- Referencias bibliográficas
[1] ISO 11664-2 2007/CIE S014-2:2006 Colorimetry – Part 2: CIE illuminants for colorimetry, 24 p. (2007).
[2] DIRECTIVE 2005/32/EC OF THE EUROPEAN PARLIAMENT AND OF THE COUNCIL of 6 July 2005, “Establishing a framework for the setting of ecodesign requirements for energy-using products and amending Council Directive 92/42/EEC and Directives 96/57/EC and 2000/55/EC of the European Parliament and of the Council,” OJ L191, 29–57 (2005).
[3] DIRECTIVE 2009/125/EC OF THE EUROPEAN PARLIAMENT AND OF THE COUNCIL of 21 October 2009, “Establishing a framework for the setting of ecodesign requirements for energy-related products,” OJ L285, 10–35 (2009).
[4] COMMISSION REGULATION (EU) No 1194/2012 of 12 December 2012, “Implementing Directive 2009/125/EC of the European Parliament and of the Council with regard to ecodesign requirements for directional lamps, light emitting diode lamps and related equipment,” OJ L342, 1–22 (2009).
[5] Colorimetry, 3rd edition, CIE Technical Report No. 15:2004, 80 p. (2004).
[6] The Basis of Physical Photometry, CIE Technical Report No. 18.2, 42 p (1983).
[7] International Commission on Illumination. Measurement of LEDs. CIE Publ. No.127:2007, Vienna: International Commission on Illumination; 2007.
[8] T. Pulli et. al., “Advantages of White LED Lamps and New Detector Technology in Photometry,” Light Sci. Appl. 4, e332 (2015).
[9] Alexander Kokka et al. “Development of white LED Illuminantes for colorimetry and recommendation of white LED reference spectrum for photometry”. Metrologia 55, 526-534 (2018).
[10] American National Standards Institute 2011 Specifications for the chromaticity of solid state lighting products, Standard ANSI NEMA C78.377-2011.
[11] Jost S, Ngo M, Ferrero A, Poikonen T, Pulli T, Thorseth A and Blattner P 2017 “Determination of illuminants representing typical white light emitting diode sources” Proc. Conf.‘Smarter Light. Better Life’ CIE Midterm Meeting pp 427–32.
[12] Colorimetry, 4th edition, CIE Technical Report No. 15:2018.
[13] Photometry Using V(λ)-Corrected Detectors as Reference and Transfer Standards, CIE Technical Report No. 210, 36 p. (2014).
[14] Sildoja M, Manoocheri F, Merimaa M, Ikonen E, Müller I et al. “Predictable quantum efficient detector: I. photodiodes and predicted responsivity”. Metrologia 2013; 50:385–394.
[15] Müller I, Johannsen U, Linke U, Socaciu-Siebert L, SmîdMet al. “Predictable quantum efficient detector: II. characterization and confirmed responsivity”. Metrologia 2013;50: 395–401.
[16] Dönsberg T, Sildoja M, Manoocheri F, Merimaa M, Petroff L et al. “A primary standard of optical power based on induced-junction silicon photodiodes operated at room temperature”. Metrologia 2014; 51: 197–202.
[17] Gran J, Kübarsepp T, Sildoja M, Manoocheri F, Ikonen E et al. “Simulations of a predictable quantum efficient detector with PC1D”. Metrologia 2012; 49: S130–S134.
[18] Sildoja M, Dönsberg T, Mäntynen H, Merimaa M, Manoocheri F et al. “Use of the predictable quantum efficient detector with light sources of uncontrolled state of polarization”. Meas Sci Technol 2014; 25: 015203.
[19] K. Lahti et. al., “Realization of the luminous-flux unit using a LED scanner for the absolute integrating sphere method,” Metrologia 37, 595–598 (2000).
[20] S. Winter et. al. “Convenient integrating sphere scanner for accurate luminous flux measurements,” Metrologia 46, S248–S251 (2009).
[21] Alexander Kokka et al. “Fisheye camera method for spatial non-uniformity corrections in luminous flux measurements with integrating spheres”. Metrologia 54 577-583 (2017).
[22] Y. Zong, “Development of a new spheregoniophotometer method,” Abstracts of the 28th CIE Session, (Manchester, UK), p. 147 (2015).









Comentarios