El nuevo Sistema Internacional de Unidades (SI), cada vez más cerca

Dr. Emilio Prieto,
Centro Español de Metrología (CEM)
Tres Cantos
Madrid

Dr. Ismael Castelazo
Centro Nacional de Metrología
CENAM
México

Resumen: La Resolución 1 adoptada por la Conferencia General de Pesas y Medidas (CGPM) en su 24ª reunión (2011) reflejó la intención del Comité Internacional de Pesas y Medidas (CIPM) de proponer una revisión del SI que ligara las definiciones del kilogramo, ampere, kelvin y mol, a valores numéricos exactos de la constante de Planck h, carga elemental e, constante de Boltzmann k y constante de Avogadro N_A, respectivamente, así como de revisar la forma de definir el SI y de formular la redacción de las unidades SI de tiempo, longitud, masa, corriente eléctrica, temperatura termodinámica, cantidad de sustancia e intensidad luminosa, tal que las constantes de referencia sobre las que se basa el SI revisado aparecieran de manera explícita.

Entre los numerosos beneficios que dicha revisión representará para la ciencia, la tecnología, la industria y el comercio, es de destacar la ligazón del kilogramo a un invariante de la naturaleza, en lugar de a la masa de un patrón materializado, garantizando así definitivamente su estabilidad a largo plazo.

El SI revisado será aprobado por la 26ª CGPM en noviembre de 2018, entrando en vigor el Día Mundial de la Metrología, 20 de mayo, de 2019.

Palabras clave: sistema internacional de unidades, SI, unidades básicas, constantes universales.

Abstract: Resolution 1 adopted by the General Conference of Weights and Measures (CGPM) at its 24^th Session (2011) reflected the intention of the International Committee of Weights and Measures (CIPM) to propose a revision of the SI to link the definitions of kilogram, ampere, kelvin and mol, to exact numerical values of the Planck constant h, elementary charge e, constant Boltzmann k and Avogadro constant N_A respectively, as well as to revise the form of defining the SI such the wording of the units of time, length, mass, electric current, thermodynamic temperature, amount of substance and luminous intensity includes explicitely the reference constants values on which the revised SI is based.

Among the many benefits that such a review will represent for science, technology, industry and commerce, it is to emphasize the linkage of the kilogram to an invariant of nature, rather than to the mass of a materialized standard, so definitively guaranteeing its long-term stability.

The revised SI will be approved by the 26^th CGPM in November 2018, coming into force the World Metrology Day, the 20 May, in 2019.

Keywords: international system of units, SI, basic units, universal constants

1.Introducción

Para conocer el mundo que nos rodea, comprender los fenómenos que en él acontecen y hacer que progresen la ciencia y la tecnología, siempre ha sido necesario medir, pero medir bien, con la máxima exactitud y la menor incertidumbre, tal como preconiza la metrología, ciencia de la medida.

Según el Vocabulario Internacional de Metrología [1], magnitud es la propiedad de un fenómeno, cuerpo o sustancia, que puede expresarse cuantitativamente mediante un número y una referencia, habitualmente una unidad de medida. Según esto, el valor Q de cualquier magnitud puede expresarse como Q = {Q} [Q], siendo {Q} su valor numérico y [Q] la unidad de medida adoptada.

La unidad de medida es pues un valor particular de la magnitud considerada, tomada como referencia, y el valor numérico, el cociente entre el valor de la magnitud considerada y la unidad elegida.

Las unidades, más concretamente sus realizaciones prácticas, se eligen de forma que se mantengan estables en el tiempo y en el espacio (idea subyacente bajo los antiguos patrones materializados), o bien sean de fácil reproducción en cualquier tiempo y lugar (actual situación de los experimentos físicos).

El establecimiento de un sistema de magnitudes, junto a un conjunto de ecuaciones que las ligue entre sí, es el paso previo a establecer el correspondiente sistema de unidades. Las ecuaciones que relacionan las magnitudes determinarán también las relaciones entre sus unidades.

El actual sistema SI es el sistema adoptado internacionalmente, utilizado en la práctica científica y el único legal en España [2], en la Unión Europea y en numerosos otros países. El SI parte de un pequeño número de magnitudes/unidades denominadas básicas definiendo, a partir de ellas, las denominadas derivadas, como producto de potencias de las básicas. Cuando este producto de potencias no incluye ningún factor numérico distinto de la unidad, estas unidades derivadas se denominan coherentes. El número de magnitudes derivadas de interés para la ciencia y la tecnología puede crecer sin límites, a medida que se desarrollan nuevos campos científicos.

La dimensión de una magnitud derivada Q, en función de las básicas, se expresa como:

dim Q = L^α M^β T^γ I^δ Θ^ε N^ζ J^η

donde las letras mayúsculas representan las magnitudes básicas y los exponentes pueden ser positivos, negativos o nulos.

P. ej., en el caso de la aceleración a, dim a = L¹ M⁰ T^-2 I⁰ Θ⁰ N⁰ J⁰ = L T^-2

La clasificación de las magnitudes y unidades en básicas y derivadas es puramente convencional y fruto de la evolución histórica del propio sistema. En el futuro, con las unidades basadas en el valor de determinadas constantes, dicha clasificación carecería de sentido y podría desaparecer.

Las magnitudes básicas del actual SI son: longitud, masa, tiempo, intensidad de corriente eléctrica, temperatura termodinámica, cantidad de sustancia e intensidad luminosa, siendo las correspondientes unidades SI: metro, kilogramo, segundo, amperio, kelvin, mol y candela.

El SI proporciona además una serie de prefijos, de gran utilidad para expresar los valores de magnitudes mucho más grandes y mucho más pequeñas que la unidad SI coherente correspondiente, permitiendo formar múltiplos y submúltiplos decimales de dichas unidades [3].

Solo el kilogramo, unidad básica de masa, constituye la excepción, al incluir, por desafortunadas razones históricas el prefijo ‘kilo’ en el nombre de la unidad. Aún así, los múltiplos y submúltiplos del kilogramo se forman añadiendo los nombres de los prefijos a la unidad ‘gramo’ y los símbolos de los prefijos al símbolo de la unidad ‘g’. Así, 10^-6 kg se escribe miligramo, mg, y no microkilogramo, µkg.

De esta forma, se mantiene la coherencia con el resto del sistema salvo, como decimos, en la impropia denominación de la unidad de masa, resultante del patrón materializado elegido en su día.

2. Evolución y Revisión del SI

En 1960 la 11ª Conferencia General de Pesas y Medidas (CGPM) definió y estableció formalmente el SI [4] en su Resolución 12, basado en el anterior sistema métrico decimal. Desde entonces se ha revisado de cuando en cuando, en respuesta a las necesidades de la ciencia y la tecnología.

El SI es un sistema coherente de unidades, que permite cuantificar cualquier magnitud medible de interés en la investigación, la industria, el comercio o la sociedad, en campos tan variados como la salud, la seguridad, la protección del medio ambiente, la adquisición de bienes o la facturación de consumos, por ejemplo.

Los Estados firmantes de la Convención del Metro representan hoy en día alrededor del 98 % de la economía mundial, por lo que el SI es la base misma del comercio internacional y el soporte de la infraestructura metrológica mundial, a través de los institutos nacionales de metrología.

El sistema de magnitudes que subyace bajo el SI, y las ecuaciones que las relacionan, tienen su base en el conocimiento que se posee sobre la naturaleza, y cualquier científico o persona involucrada en cualquiera de las ramas del conocimiento científico, incluyendo la enseñanza en cualquiera de sus niveles, debe estar familiarizada con él.

La Resolución 1 adoptada por la CGPM en su 24ª reunión de 2011 hizo suya la propuesta del Comité Internacional de Pesas y Medidas (CIPM), sobre la posibilidad de revisar el SI, de forma que las definiciones del kilogramo, amperio, kelvin y mol quedaran ligadas a valores numéricos bien conocidos de determinadas constantes. También debería revisarse la redacción de las definiciones de las unidades SI, de forma que en ellas aparecieran de manera explícita las constantes utilizadas para renovar el SI [5].

Esta revisión del SI surge en respuesta a las nuevas exigencias científico-tecnológicas, que requieren aún menores incertidumbres de medición en todos los campos, para poder garantizar con la mayor seguridad, tanto hipótesis de partida de teorías físicas, como los valores de otras constantes de la naturaleza, o las pequeñísimas tolerancias de fabricación exigidas hoy en día en la industria o en el campo de las nanotecnologías.

Al apoyarse en valores de constantes universales, éstas se tomarán como exactas, transfiriéndose su incertidumbre a la unidad correspondiente.

Por supuesto, el nuevo SI revisado no supondrá cambio alguno en nuestra vida diaria, garantizándose la continuidad de todo lo existente hasta ahora. Únicamente los laboratorios nacionales, que realizan mediciones de gran exactitud y baja incertidumbre, deberán quizá retocar alguna de sus realizaciones prácticas. Igualmente, los libros de texto deberán recoger el SI revisado a fin de divulgarlo, incluyendo los valores actualizados de las constantes universales, la nueva redacción de las definiciones de las unidades, las realizaciones prácticas de éstas, etc., e insistir en su utilización universal, conforme a sus propias reglas de uso.

Entre los numerosos beneficios que la revisión del SI representa para la ciencia, la tecnología, la industria y el comercio, destaca la ligazón del kilogramo a un invariante de la naturaleza, como es la constante de Planck h, en lugar de a la masa de un patrón materializado, garantizando así definitivamente tanto el conocimiento de su valor “absoluto”, como su estabilidad a largo plazo. Esto permitirá el que todas las unidades, dada su ligazón a constantes universales, cuenten con realizaciones prácticas reproducibles en cualquier tiempo y lugar, alejadas de los anteriores patrones materializados, cuya propiedad fundamental debía ser la estabilidad a lo largo del tiempo pero que, como en el caso del kilogramo, han mostrado sus limitaciones.

La Resolución 1 de la CGPM en su 24ª reunión de 2011, a la que nos hemos referido antes, proponía ligar las definiciones del kilogramo, amperio, kelvin y mol, a valores numéricos exactos de la constante de Planck h, carga elemental e, constante de Boltzmann k y constante de Avogadro N_A, respectivamente.

Sin embargo, la Resolución 1 de la CGPM, en su 25ª reunión de 2014 [6], consideró que, a pesar de los progresos realizados hasta entonces, los datos disponibles sobre la determinación de h,e, k y N_A y de sus incertidumbres, aún no eran lo suficientemente robustos como para poder adoptar la revisión del SI, por lo que animaba a los Institutos Nacionales de Metrología (INM) y a otros entes e instituciones científicas y académicas, a continuar con sus esfuerzos para obtener datos relevantes, hasta obtener las incertidumbres y el nivel de coherencia deseado, de modo que la CGPM pudiera adoptar la resolución para reemplazar el actual SI.

3. Criterios previos a la revisión del SI

Para poder aprobar el nuevo SI revisado, los distintos comités consultivos del CIPM establecieron unos criterios previos los cuales pretendían, por una parte, mantener la continuidad del propio SI y, por otra, determinar los valores de las constantes sobre las que fundamentar el nuevo SI, con las menores incertidumbres posibles, ya que éstas pasarían a ser las incertidumbres iniciales de las nuevas unidades.

Así, para el caso de la unidad de masa, que el CIPM y la CGPM habían decidido basar en la constante de Planck h, dichos criterios eran [7]:

• Que al menos tres experimentos independientes, incluyendo el de la balanza de potencia de Kibble y el de la esfera de Silicio, permitieran determinar el valor de h con una incertidumbre relativa u_r(h) inferior o igual a 5 x 10^-8.
• Que al menos uno de dichos experimentos contara con una incertidumbre relativa u_r(h) inferior o igual a 2 x 10^-8.
• Que se hubiera comparado el actual prototipo del kilogramo internacional (KPI) con el nuevo juego de masas del BIPM, con la esfera de Silicio y con las masas utilizadas en las balanzas de potencia de Kibble, conforme a las reglas del CIPM
• Que, para la posterior circulación del kilogramo, las distintas realizaciones prácticas (mises-en pratique) hubieran sido validadas conforme a los principios del Acuerdo de Reconocimiento Mutuo del CIPM (ARM-CIPM).

Por su parte, para implantar la nueva definición del kelvin, que debía basarse en el valor de la constante de Boltzmann k, el CCT requirió [8]:

• una incertidumbre relativa u_r(k) en la determinación de k, inferior a 1 x 10^-6
• que la determinación de k estuviera basada en al menos dos métodos diferentes, cada uno de los cuales tuviera al menos un resultado con incertidumbre típica relativa inferior a 3 × 10⁻⁶.

4. Experimentos para la obtención de los valores de las constantes

Para poder cumplir estos criterios, hace años que están en marcha múltiples experimentos que proporcionan los datos con los que obtener el mejor valor de las constantes de interés, tras el ajuste de los mismos por el Comité de datos para la ciencia y la tecnología (CODATA).

Entre ellos podemos citar, en relación con la determinación de la constante de Planck h, el de la balanza de potencia o balanza de Kibble, denominada así en homenaje y reconocimiento de Bryan Kibble quien, en 1974, ya lanzó la idea de esta balanza. En relación con la determinación de la constante de Avogadro N_A, el experimento en marcha es el de la esfera de Silicio, conocido también como XRCD (X-ray crystal density).

4.1 Experimento de la balanza de potencia de Kibble [9]

La balanza de potencia de Kibble permite igualar la potencia mecánica a la eléctrica, determinando el valor de h en función de la masa m utilizada en la balanza y de otras unidades obtenidas experimentalmente con muy baja incertidumbre, como son el metro y el segundo.

Figura 1. Experimento de la balanza de potencia (de Kibble) para la determinación de h.

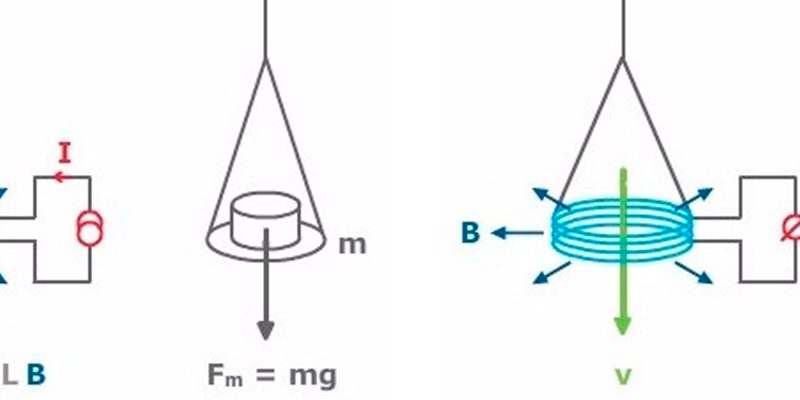
En la fase estática del experimento, la fuerza ejercida por la gravedad sobre la masa m; es decir, su peso, igual a mg, se contrarresta con la fuerza de Lorentz producida en una bobina de longitud L recorrida por una intensidad I, suspendida dentro de un campo magnético radial B (ILB), de donde mg = ILB.

En la fase dinámica, la bobina se mueve verticalmente con velocidad constante v, dentro de un campo magnético radial B, originando una tensión U, de valor LBv.

Igualando entre sí el valor LB de ambas expresiones, se obtiene mgv = UI.

En la parte izquierda de la igualdad, g se determina utilizando un gravímetro absoluto, y la velocidad v mediante interferometría láser.

En la parte derecha, U se determina con baja incertidumbre mediante un patrón de tensión basado en el efecto Josephson, tal que:

dondeC₁ es el coeficiente de calibración,

h/2e = 1/K_J es la inversa de la constante de Josephson,

f_J es la frecuencia de irradiación de la unión Josephson, y

n es el número del escalón de tensión constante generado en la unión.

Por su parte, la intensidad I se determina a partir de la caída de tensión U_R = C₂ (h/2e)·n’·f_J’ en una resistencia R calibrada frente a una resistencia Hall cuántica, tal que

dondeC₃ es el coeficiente de calibración,

h/e² = R_K es la constante de von Klitzing, y

R_H es el valor de la resistencia Hall cuántica correspondiente a la meseta i

con lo que:

y agrupando

o bien

4.2 Experimento de la esfera de Silicio

La constante de Avogadro N_A es la constante física fundamental que relaciona cualquier magnitud a escala atómica con su correspondiente a escala macroscópica, representando el número de partículas elementales (usualmente átomos o moléculas) contenidos en un mol de cualquier sustancia. Precisamente, la nueva definición del mol se basará en la mejor determinación de N_A y enfatizará la distinción entre “cantidad de sustancia” y “masa”.

Para la determinación de N_A se sigue el experimento XRCD (X-ray crystal density) [10], que trata de contar el número de átomos contenidos en una esfera de 1 kg, de ²⁸Si con una pureza del 99,995 %, aprovechando su disposición ordenada en el cristal.

Pero el objetivo del experimento es en realidad doble; por un lado, obtener el valor de N_A con una incertidumbre típica relativa u_r(N_A) inferior a 2 × 10⁻⁸ (lo que equivale a contar 100 millones de átomos y errar en 2) y por otro, determinar la masa de la esfera, de manera independiente a otras referencias de la misma magnitud, y emplearla para obtener una verificación, por esta vía, del valor de la constante de Planck h que resulta del experimento de la balanza de Kibble.

La determinación del volumen de la esfera, a partir de la medición de múltiples diámetros, y de su defecto de esfericidad, se realiza mediante interferometría láser de Fizeau. Aunque el Silicio cristalino presenta una estructura cúbica, se eligió un artefacto de forma esférica por adaptarse mejor a la instrumentación específica utilizada para caracterizar el volumen, que permite obtener la menor incertidumbre.

En el experimento XRCD se mide el espaciamiento a = d₂₂₀ (arista de la celda unidad) de la red del silicio, del orden de 0,543 nm, mediante difracción de rayos X, obteniéndose el nº de átomos en la esfera como 8 veces el cociente entre el volumen de la esfera y el de la celda unidad, dado que esta, debido a la disposición de los átomos, contiene 8.

Figura 2. Esfera de ²⁸Si utilizada en el experimento XRCD

A su vez, la masa de la esfera se puede obtener como el producto del número de átomos por la masa de cada átomo, siendo ésta igual a la masa molar dividida por la constante de Avogadro:

La masa molar M_Si contabiliza los tres isótopos del Silicio, de forma que  , donde i representa a cada isótopo (²⁸Si,²⁹Si y ³⁰Si), y f_i a la respectiva fracción molar. Aunque la primera versión del experimento utilizaba Silicio natural, con fracciones f₂₈ = 0,922, f₂₉ = 0,047 y f₃₀ = 0,031, la última versión utiliza ²⁸Si altamente enriquecido, con f₂₈ ≈ 0,999 95, por lo que  .

La constante de Avogadro se puede eliminar empleando la fómula de la constante de Rydberg [11], de manera que se obtenga una expresión en términos de la constante de Planck h y de otros parámetros que se conocen con muy buena exactitud [12], quedando:

donde los factores de la derecha de la ecuación (velocidad de la luz en el vacío c, constante de la estructura fina α, constante de Rydberg , masas atómicas relativas de los isótopos del silicio y del electrón A_rⁱ y A_r^e, y las fracciones molares f_i) se conocen con incertidumbres relativas inferiores a 1 x 10^-9 o incluso nulas (c).

Si en la ecuación anterior se despeja h y se emplea la masa de la esfera medida con trazabilidad al kilogramo patrón, es posible obtener una verificación del valor de la constante de Planck que resulta del experimento de la balanza de Kibble.

Los valores de las distintas constantes y sus incertidumbres, según el ajuste realizado por CODATA en 2014, sobre datos procedentes de estos y otros experimentos no presentados aquí, son los siguientes: [13]

Tabla 1. Valores CODATA 2014 recomendados para h,e,k y N_A. Entre paréntesis, los valores de las incertidumbres típicas asociadas.

Como puede apreciarse, todas las incertidumbres son ya inferiores a las exigidas en los anteriores criterios, y es esperable que puedan reducirse aún más, lo que por fin hace viable la aprobación del SI revisado por parte de la CGPM.

A la vista de ello, se ha establecido el 1 de julio de 2017 como la fecha de cierre de los datos que contribuirán a la determinación de los valores numéricos exactos de las constantes h, e,k y N_A por parte de CODATA. De esta forma, el SI revisado podrá ser aprobado por la 26ª CGPM en noviembre de 2018, demorándose su entrada en vigor hasta el 20 de mayo de 2019, con objeto de hacerla coincidir con el Día Mundial de la Metrología [14].

Posteriormente, el siguiente ajuste CODATA 2018 se basará en el SI revisado, lo que afectará significativa y positivamente a las incertidumbres de muchas otras constantes. Los datos a considerar para este ajuste deben haber sido publicados o enviados para publicación, antes del 31 de diciembre de 2018.

A resultas de todo lo anterior, el CCU ha preparado una propuesta de resolución, para su aprobación por la 26ª CGPM de 2018, en la que el SI revisado quedaría definido como aquel en el que:

• la frecuencia de la transición hiperfina del estado fundamental no perturbado del átomo de cesio 133, Δν_Cs, es 9 192 631 770 Hz,
• la velocidad de la luz en el vacío, c, es 299 792 458 m/s,
• la constante de Planck, h, es 6,626 070 15 x 10^-34 J s,
• la carga elemental, e, es 1,602 176 634 x 10^-19 C,
• la constante de Boltzmann, k, es 1,380 649 x 10^-23 J/K
• la constante de Avogadro, N_A, es 6,022 140 76 x 10²³ mol^-1,
• la eficacia luminosa de la radiación monocromática de 540 x 10¹² Hz, K_cd, es 683 lm/W.

con los anteriores valores numéricos carentes de incertidumbre y donde las unidades hercio, julio, culombio, lumen y vatio, con símbolos Hz, J, C, lm y W respectivamente, están relacionadas con las unidades segundo, metro, kilogramo, amperio, kelvin, mol y candela, con símbolos s, m, kg, A, K, mol y cd respectivamente, por las expresiones Hz = s^–1, J = m² kg s^–2, C = A s, lm = cd m² m^–2 = cd sr y W = m² kg s^–3.

Las nuevas definiciones del kilogramo (kg), amperio (A), kelvin (K) y mol (mol) estarán referenciadas, respectivamente, a las constantes fundamentales h, e, k y N_A.

Todas las definiciones de las unidades, tanto las citadas anteriormente como las del metro (m), segundo (s) y candela (cd) se redactarán de forma distinta a la actual, de manera que las constantes anteriores aparezcan en ellas de manera explícita, y las unidades resulten implícitamente definidas al fijar el valor numérico de dichas constantes.

5. Conclusiones

La revisión del SI, base del comercio internacional y soporte de la infraestructura metrológica global, en respuesta a las nuevas exigencias científico-tecnológicas de nuestro tiempo, será aprobada por la CGPM en su reunión nº 26, en noviembre de 2018.

Dicha revisión definirá las unidades del SI en base a constantes universales bien determinadas. Entre los numerosos beneficios que esta revisión representará para la ciencia, la tecnología, la industria y el comercio, destaca la ligazón del kilogramo a un invariante de la naturaleza, como es la constante de Planck h, en lugar de a la masa de un patrón materializado, garantizando así definitivamente tanto el conocimiento de su valor “absoluto”, como su estabilidad a largo plazo.

Además, permitirá que todas las unidades cuenten con realizaciones prácticas reproducibles en cualquier tiempo y lugar, superando definitivamente la fase de los patrones materializados.

El nuevo SI no supondrá cambio alguno en nuestra vida diaria, garantizándose la continuidad de lo existente hasta ahora. Únicamente los laboratorios nacionales, que realizan mediciones de gran exactitud y baja incertidumbre, deberán quizá ajustar algunas de sus realizaciones prácticas. Pero sí es importante que los libros de texto recojan cuanto antes este cambio, a fin de divulgarlo a la sociedad, además de seguir haciendo hincapié en la universalidad del SI y en su correcta utilización, conforme a sus propias reglas de uso, en todos los niveles de la enseñanza.