Estefanía de Mirandés
Bureau International des Poids et Mesures
Resumen:
El 20 de mayo de 2019 fue un día especialmente señalado para los metrólogos del mundo entero, ya que entró en vigor una reforma histórica del Sistema Internacional de Unidades, SI. A partir de esta fecha, todas las unidades del SI están definidas a partir de constantes de la naturaleza, no quedando ya ninguna unidad vinculada a un artefacto material.
La definición central del SI revisado no comporta una definición explícita de las unidades básicas, como era el caso en precedentes versiones, sino una especificación del valor numérico exacto de siete constantes fundamentales de la naturaleza. Ello define implícitamente las unidades del sistema, sin establecer una jerarquía entre unidades básicas y unidades derivadas.
Los valores numéricos escogidos para esas constantes garantizan la continuidad entre las anteriores unidades y las unidades redefinidas, de forma que el usuario final no perciba ningún cambio en la vida cotidiana. Sólo los laboratorios trabajando con alta precisión notarán algún cambio, en particular en el área eléctrica y de masa. Para ello ha sido necesario medir dichas constantes en el sistema precedente con gran precisión antes de proceder al cambio.
La estructura del Tratado del Metro de 1875 ha resistido impecablemente el paso del tiempo y ha establecido una estructura metrológica internacional que ha permitido construir un sistema de unidades capaz de adaptarse al paso del tiempo sin perder sus características esenciales.
En el nuevo marco, tras el SI revisado, la Oficina Internacional de Pesas y Medidas (BIPM) continuará ejerciendo el rol de coordinador de la metrología mundial y garante de la uniformidad mundial de las unidades de medida y su diseminación. Para ello, seguirán siendo esenciales las comparaciones clave entre los Institutos Nacionales de Metrología firmantes del CIPM MRA (Acuerdo de Reconocimiento Mutuo del CIPM, 1999).
Palabras clave: Sistema Internacional, redefinición, unidades de medida, constantes universales.
Abstract:
May 20 2019 was a day especially marked for metrologists worldwide, as a historic reform of the International System of Units, the SI, came into effect. As of this date, all SI units are defined from constants of nature, with no unit linked to a material artifact.
The central definition of the revised SI does not imply an explicit definition of the basic units, as was the case in the previous version, but a specification of the exact numerical value of seven fundamental constants of nature. This implicitly defines the units of the system, without establishing a hierarchy between basic units and derived units.
The numerical values chosen for these constants guarantee the continuity between the previous units and the redefined units and so the end user does not perceive any change in daily life. Only laboratories working with high precision will notice any change, particularly in the electrical and mass areas. For this, it has been necessary to measure these constants in the preceding system with great precision before proceeding with the change.
The structure of the Treaty of the Metre, 1875, has impeccably resisted the passage of time and has established an international metrological structure that has allowed the construction of a system of units capable of adapting to the passage of time without losing its essential characteristics.
In the new framework, after the revised SI, the International Bureau of Weights and Measures (BIPM) will continue playing the role of coordinator of the global metrology and guarantor of the global uniformity of the units of measure and their dissemination. To this aim, key comparisons between all the National Metrology Institutes that signed CIPM MRA (CIPM Mutual Recognition Agreement, 1999) will continue to be essential.
Keywords: International System, redefinition, units of measurement, universal constants.
1. Introducción
El 20 de mayo de 2019 fue un día especialmente señalado para los metrólogos del mundo entero, ya que entró en vigor una reforma histórica del Sistema Internacional de Unidades, el SI. A partir del 20 de mayo todas las unidades del SI están definidas a partir de constantes de la naturaleza, no quedando ya ninguna unidad vinculada a un artefacto material. Esta desmaterialización de las unidades supone una apuesta por la estabilidad a largo plazo de sus definiciones y la universalidad del acceso a las mismas, dos características que unidades basadas en artefactos materiales no podían garantizar [Stock 2019].
En particular, el 20 de mayo nos despedimos del Prototipo Internacional del Kilogramo, conocido como “el gran K”, un cilindro de platino iridio conservado en el Bureau International des Poids et Mesures (BIPM), en Francia, cuya masa ha definido el kilogramo desde 1889. Este prototipo es el último artefacto material que ha servido para definir una unidad del SI [Davis 2003].
La ambición de ligar nuestras unidades de medida a parámetros universales no es reciente. La idea se remonta a la revolución francesa, en la que el clamor popular exigía unidades de medida que no dependieran de la situación geográfica ni variasen en el tiempo. Ello condujo al nacimiento del sistema métrico decimal con el lema “A tous les temps, à tous les peuples” (para todos los tiempos, para todos los pueblos). El Sistema Internacional es el digno heredero del sistema métrico decimal y ha hecho suya la aspiración de establecer un sistema de unidades verdaderamente universal e imperecedero. Este artículo mostrará las principales etapas de la aventura de la desmaterialización de nuestras unidades de medida.
2. Los orígenes. Nacimiento del sistema métrico decimal
Los orígenes del sistema métrico decimal se encuentran en Francia. Antes del siglo XVIII, nunca hubo en Francia un sistema de unidades unificado. A pesar de los repetidos intentos de Carlomagno y diversos reyes posteriores que intentaron reducir el número de unidades de medida utilizadas, en 1795 Francia contaba con más de setecientas unidades de medida diferentes. Muchas de ellas tomaban como referencia criterios de la anatomía humana: la palma, el pie, el codo, la toesa, etc. Esas unidades presentaban además valores diferentes de una ciudad a otra, de una corporación a otra, y a menudo dependían también del tipo de objeto que se medía. Las medidas de volumen y las de longitud no tenían vinculación alguna entre ellas. Los múltiplos y submúltiplos de las unidades no seguían una estructura armoniosa. Todo ello dificultaba enormemente los cálculos en la vida cotidiana, introducía errores y era fuente de engaños. Esta situación limitaba también el desarrollo de innovaciones científicas. Por ello, a medida que la industria y el comercio empezaron a generalizarse, la necesidad de una armonización se impuso con fuerza [Quinn 2011].
El clima de reforma que sucedió a los acontecimientos revolucionarios en Francia se revelaría muy propicio para precipitar una reforma de las unidades de medida. Los “cuadernos de quejas” (cahiers de doléances), que registraban las peticiones y quejas del pueblo en la Francia del antiguo régimen para ser debatidas en las asambleas de los Estados Generales, recogían numerosísimas reclamaciones de unidades de medida universales que permitieran liberarse de la arbitrariedad de las unidades de medida señoriales de la época.
Tayllerand, influyente político y diplomático, propuso a la Asamblea la constitución de una comisión de sabios encargada de establecer la base de un nuevo sistema de unidades que asegurara la invariabilidad de las medidas tomando como nuevas referencias patrones universales basados en fenómenos naturales. La comisión fue establecida el 16 de febrero de 1791 y estuvo compuesta por científicos de gran renombre como Borda, Condorcet, Laplace, Lagrange y Monge. Su primera tarea fue dirimir entre tres posibles referencias para establecer una nueva definición del metro: la longitud de un péndulo simple oscilando en una latitud de 45° con un período de un segundo, la longitud de un cuarto del círculo máximo del ecuador o la longitud de un cuarto del meridiano terrestre. El péndulo presentaba el inconveniente de que el período de su oscilación dependía de su posición en el globo terrestre a causa de las variaciones espaciales de la fuerza de la gravedad. La longitud del péndulo hubiera necesitado de ajustes en función de la fuerza local de la gravedad y ello lo hacía impráctico. La longitud de un cuarto del círculo máximo del ecuador carecía de universalidad ya que dicho círculo no cruzaba por todos los países. La solución del meridiano fue seleccionada por su universalidad ya que todo país contaba con un meridiano que lo atravesaba y podía acceder, en principio, a la definición. El 26 de marzo del 1791 nacía así el metro, con una longitud definida como el diez millonésimo del cuarto del meridiano terrestre. El meridiano terrestre se definía en aquel entonces, siguiendo los criterios de los astrónomos, como un círculo completo alrededor de la Tierra. Esta definición resulta admirable por no contener ningún objeto ni parámetro arbitrario ni propio a la situación geográfica de ningún pueblo en el globo. El principio de universalidad, que sería generalizado en el futuro a todas las unidades, cristalizaba así por primera vez.
La nueva definición del metro fue aceptada, pero el verdadero desafío de establecer la longitud exacta del cuarto del meridiano terrestre acababa de empezar. Ello dio lugar a una fascinante odisea para efectuar las mediciones necesarias, que fue llevada a cabo por dos expertos en geodesia que recibieron el encargo de la comisión: Pierre-François Mechain (1744 – 1804) y Jean-Baptiste Delambre (1749 – 1822) [Adler, 2003]. Estos dos científicos asumieron solos la imponente tarea de medir la longitud del meridiano desde Dunkerke hasta Barcelona usando la técnica de la triangulación. Les llevaría siete años concluir las medidas. La triangulación es una técnica ingeniosa que consiste en jalonar el itinerario que se quiere medir de una red de puntos escogidos por su visibilidad (torres, campanarios, cimas, etc.). Esos puntos debían ser escogidos por formar triángulos yuxtapuestos. Usando cálculos trigonométricos es posible, si se conocen todos los ángulos formados por dos triángulos adyacentes y la longitud de por lo menos uno de los lados de uno de los dos triángulos, calcular la longitud de todos los lados de los dos triángulos. Para la determinación de los ángulos con suficiente precisión, Méchain y Delambre utilizaron el innovador círculo repetidor de Borda, que permitía obtener incertidumbres de cerca de un segundo, cuando los cuartos de círculo astronómicos que se utilizaban hasta entonces permitían incertidumbres de unos 15 segundos. Las medidas de longitud a nivel del suelo se hicieron con reglas bimetálicas de cobre-platino que tenían por unidad la toesa de Perú. La Academia de Ciencias francesa repartió la medida del meridiano encargando los dos tercios superiores, desde Dunkerque hasta Rodez, a Delambre y el tercio inferior, desde Rodez hasta Barcelona, a Méchain. Esta desproporción se justificó argumentando que Delambre debería pasar por puntos donde antiguas triangulaciones ya habían sido realizadas mientras que Méchain debía penetrar en terreno virgen de medidas geodésicas anteriores. Desafortunadamente, muchas de las referencias de triangulaciones anteriores se revelaron inutilizables, ya que, en medio de la agitación revolucionaria, torres y campanarios habían sido derribados o se encontraban en ruinas. El periplo de Méchain y Delambre estuvo sembrado de acontecimientos singulares: arrestos, revocaciones temporales e incluso destrucción parcial de sus resultados geodésicos ya que sus actividades suscitaban el recelo de la población. Una parte de las medidas debía efectuarse en territorio español y en 1793 estalló la guerra entre España y Francia. Entre 1793 y 1795, la instauración del terror ralentizó sus trabajos.
En paralelo a sus medidas, el metro fue definido provisionalmente en Francia con la ley del 1 de Agosto de 1793 usando antiguas medidas del meridiano francés que habían sido realizadas por Cassini y que habían sido publicadas en 1758. Esta definición del metro fue temporal, a la espera de los resultados de Méchain y Delambre, que se concluirían en 1798 y conducirían en 1799 a definir el patrón definitivo del metro.
Una vez que la unidad de longitud estuvo definida a partir de un parámetro universal, el resto de unidades se definieron a partir del metro para beneficiarse de esa misma universalidad. Así se definieron el metro cuadrado, el metro cúbico, y la unidad de masa. Para definir la unidad de masa, la comisión eligió establecer que el “grave” (que más tarde pasaría a llamarse kilogramo) sería igual a la masa de un decímetro cúbico de agua pura a la temperatura de máxima densidad. La comisión prefirió basar la definición en el agua, y no en otros elementos como el mercurio o el oro, argumentando la facilidad de acceder a ella y de destilarla. Nacía así el sistema métrico decimal instituido por la ley “de pesas y medidas” francesa el 7 de abril de 1795. Como su nombre indica, el sistema métrico introdujo la decimalización, que implicaba que el paso a un múltiplo o un submúltiplo del metro se realizaba simplemente deslizando la coma decimal una cifra.
Estas definiciones universales necesitaron entonces ser acercadas a la población para permitir la generalización de su uso. Para ello, en 1799, ya con los resultados definitivos de Méchain y Delambre se fabricaron un prototipo material de platino, de longitud igual a un metro y un cilindro también de platino, de masa igual a un kilogramo. Fueron depositados en los Archivos de la República, en París, donde todavía siguen, y fueron dedicados “a todos los tiempos, a todos los hombres”. Diversas copias fueron puestas a disposición de la ciudadanía.
3. Internacionalización del sistema métrico decimal. La Convención del metro. Nacimiento del BIPM. Prototipos internacionales del kilogramo y del metro.
El sistema métrico decimal, que contenía la simplicidad y la universalidad en su concepción empezó a propagarse fuera de Francia. El desarrollo de redes ferroviarias, el auge de la industria y la multiplicación de intercambios comerciales crearon la exigencia de precisión en las medidas. Desde principios del siglo XIX el sistema métrico fue adoptado en diversas provincias italianas. Fue declarado obligatorio en los Países Bajos en 1816 y escogido por España en 1849.
En Francia, tras la adopción de algunas medidas contradictorias debido a controversias políticas, la ley del 4 de julio de 1837 adoptó exclusivamente el sistema métrico decimal, medio siglo más tarde de su creación, impulsada por el entusiasmo revolucionario.
A partir de 1860 las adhesiones se multiplicaron abarcando incluso países latinoamericanos. Sin embargo, todos esos países quedaban subordinados a Francia para obtener copias exactas de los prototipos del metro y del kilogramo. Esta dependencia reforzó la iniciativa de establecer un organismo internacional neutral encargado de conservar nuevos prototipos internacionales y de facilitar sus copias a los países miembros. Así nace en 1875 el Bureau International des Poids et Mesures (BIPM), con sede en Sèvres, a las afueras de París, creado a través del Tratado del Metro, firmado el 20 de mayo de 1875 en París durante una conferencia diplomática por los representantes de 17 estados signatarios, entre ellos España. Fue notable la ausencia de Gran Bretaña entre los signatarios e igualmente notable la presencia de Estados Unidos. Gran Bretaña firmaría el tratado en 1884.
La misión inicial del BIPM fue la de fomentar el establecimiento del sistema métrico en el mundo y asegurar su uniformidad, favoreciendo así el progreso de la metrología en todos los campos. Se decidió que se fabricarían nuevos prototipos internacionales del metro y del kilogramo en platino-iridio replicando los patrones legales franceses y utilizando las mejores técnicas de las que se disponían en aquel momento.
El Tratado del Metro estableció igualmente una nueva estructura metrológica permanente que permitiría a los estados signatarios actuar conjuntamente en todos los asuntos relacionados con las unidades de medida. Tres órganos fueron creados para ello:
- La Conferencia General de Pesas y Medidas (Conférence Générale des Poids et mesures o CGPM), que es la conferencia diplomática en la que se ejerce la toma oficial de decisiones. Se reúne cada cuatro años en Francia.
- El Comité Internacional de Pesas y Medidas (Comité International des Poids et Mesures, CIPM), formado por dieciocho personas elegidas nominativamente por la CGPM, cada uno de un estado miembro diferente. Este comité se ocupa de someter a la consideración de la CGPM resoluciones proponiendo mejoras relativas a las unidades y a sus definiciones. Para ello se apoya en el trabajo de Comités Consultivos formados por expertos internacionales en diferentes áreas de la metrología.
- La Oficina Internacional de Pesas y Meddidas (Bureau International des Poids et Mesures, BIPM), bajo supervisión directa del CIPM, encargado de conservar los prototipos internacionales, de fabricar copias de ellos para los estados miembros y de llevar a cabo comparaciones periódicas de los mismos.
Cabe destacar que el primer presidente del CIPM fue un español, el general Carlos Ibáñez e Ibáñez de Íbero (1825 – 1891) que estuvo 16 años en dicho cargo. Ibáñez fue un oficial militar con gran inclinación científica y matemática que revolucionó la geodesia al inventar un nuevo aparato (conocido como “aparato Ibáñez”) con el que midió la base central de triangulación geodésica de España con una precisión inaudita. La fama de su instrumento se extendió rápidamente, no sólo en España, sino en toda Europa. Ello le condujo a ser director del nuevo instituto geográfico español y más tarde a ser nombrado Marqués de Mulhacén. La designación de Mulhacén tomó su origen en la susodicha montaña que Ibáñez de Ibero utilizó para realizar una triangulación que le permitiría conectar África con España.
El Tratado del Metro sería modificado en 1921. Actualmente, cuenta con 59 estados miembros y 42 estados asociados, que corresponden a la mayoría de países industrializados.
El Tratado del Metro requería la fabricación de un nuevo prototipo internacional del metro y otro del kilogramo. En 1879, Johnson Matthey fabricó tres cilindros de una nueva aleación de Pt-Ir (Platino Iridio), en vez de Pt sólo como en el caso de los patrones franceses. Así se escogió porque el iridio daba a la aleación una gran dureza y resistencia al posible deterioro debido al uso. También resultaba muy resistente a la oxidación y al deslustre. Los cilindros medían unos 39 mm de diámetro y de altura, y pesaban poco más de un kilogramo. El kilogramo de los archivos franceses fue puesto a disposición y se procedió a pulir con gran cuidado los tres prototipos en Pt-Ir para acercar su masa lo más posible a la del patrón francés. A. Collot, el artesano encargado del pulido consiguió que uno de los tres cilindros se aproximase tanto al patrón francés que las mejores medidas de comparación que se llevaron a cabo en 1881 fueron incapaces de distinguir entre la masa de ambos. Ese cilindro fue escogido como el futuro prototipo internacional del kilogramo. Las comparaciones de masa se llevaron a cabo en aire, no en el vacío, para evitar someter al patrón francés a un proceso que le hubiera hecho variar significativamente su masa por desgasificación [Quinn 2011].
En cuanto al patrón internacional del metro, en 1881 se llevaron a cabo comparaciones entre la longitud del metro de los Archivos franceses y la del futuro patrón internacional y se le grabaron sendas marcas en sus extremos para denotar que la longitud entre ellas era de un metro. Las comparaciones en aire se realizaron con un aparato de Fizeau. Las comparaciones a 0 grados centígrados tuvieron que esperar a que las temperaturas exteriores disminuyeran. Se hicieron mediciones a diversas temperaturas y se calculó el coeficiente de expansión térmico de ambos prototipos.
La siguiente etapa fue la de fabricar suficientes copias de los prototipos del metro y del kilogramo para suministrar a todos los estados signatarios del Tratado del Metro. Cuarenta cilindros destinados a ser futuros prototipos nacionales del kilogramo fueron entregados en 1884 al BIPM donde su densidad fue evaluada por pesada hidrostática y fueron pulidos hasta obtener una masa de un kilogramo con una tolerancia de más o menos un miligramo. Las comparaciones de masa entre todos los nuevos prototipos y el prototipo patrón se prolongaron desde 1886 hasta 1888. La incertidumbre de calibración dada fue de dos microgramos. La fabricación de los prototipos nacionales del metro tomó más tiempo que la de los kilogramos debido a que la forma de las barras no era de fabricación sencilla, ya que se escogió que su sección transversal presentara forma de X, y el proceso de grabado y pulido era también complejo. Las comparaciones finales entre la longitud de los prototipos y la del metro internacional concluyeron en 1889.
A finales de 1888, el avance del trabajo justificó la convocatoria de la primera Conferencia General de Pesas y Medidas para 1889. Se reunió en el Pavillon de Breteuil del BIPM donde se adoptaron las definiciones oficiales de los nuevos prototipos internacionales del metro y el kilogramo y se distribuyeron las copias a los estados signatarios. Cuatro copias del kilogramo y cinco del metro quedaron atribuidas al BIPM. El cierre de la Conferencia el 28 de septiembre de 1889 marcó el final del primer período de existencia del BIPM. Todo lo planeado en los años que precedieron al Tratado del Metro había sido llevado a la práctica. El BIPM entraba entonces en una segunda etapa que se revelaría de importante trabajo científico y que vería la creación de los grandes laboratorios nacionales de metrología.
4, El metro
La primera y única comparación de las copias nacionales del metro con el prototipo internacional se llevó a cabo entre 1921 y 1936 y concluyó que las longitudes eran equivalentes dentro de un margen de 0,2 micrómetros. En paralelo, la óptica interferométrica empezó a desarrollarse y a ser utilizada en medidas de longitud cada vez más largas. En 1921 ya se anunciaba que estas nuevas técnicas de medida podrían permitir uniformizar las medidas de longitud mundialmente. En particular, ciertas líneas espectrales del Cadmio y del Kriptón aparecían como las más adecuadas. La precisión de las medidas realizadas por Albert Michelson, Jean-René Benoit y Fabry y Perot utilizando la línea roja del Cadmio (λCd ≈ 644 mn) para medir la longitud del prototipo internacional del metro en el BIPM condujeron al CIPM en 1927 a adoptar el Angstrom como unidad secundaria de longitud para medidas espectroscópicas. La definición dada fue [CIPM]:
λCd = 6438,4696 Angstroms
El trabajo de Michelson relativo a la medición de la longitud del prototipo internacional del metro por debajo de λ/10 fue una de las razones que motivaron su premio Nobel de física en 1907. Durante los años 50, el Angstrom se convirtió rápidamente en la unidad natural para expresar medidas espectroscópicas. Sin embargo, la conversión del Angstrom al metro añadía una incertidumbre elevada. La solución residiría en definir el metro también por métodos interferométricos. Los avances espectroscópicos habían demostrado que la línea roja del Cadmio contenía en realidad un grupo de líneas muy cercanas las unas de las otras debido a la presencia de ocho isótopos en el Cadmio natural. Para obtener una línea precisa era necesario recurrir a un elemento mono-isotópico. A temperatura ambiente, se vio que el Kriptón era un gas que permitía un enriquecimiento isotópico sencillo. La línea naranja del isótopo 86 de Kriptón (λ ≈ 606 mn) fue elegida como referencia tras compararla en el vacío con la línea roja del Cadmio, que a su vez había sido comparada con el prototipo internacional del metro. En 1960, la undécima Conferencia General de Pesas y Medidas adoptó una nueva definición del metro que rezaba [CGPM]
“El metro es la longitud igual a 1 650 763,73 longitudes de onda en el vacío de la radiación correspondiente a la transición entre los niveles 2p10 y 5d5 del átomo de Kriptón 86”.
En los años 60 una nueva invención empezó a superar a la lámpara de descarga de Kriptón como referencia básica en interferometría: el láser, que presentaba dos ventajas sustanciales sobre la luz de una lámpara de descarga, su monocromaticidad y su coherencia. Los límites de la definición en vigor se pusieron de manifiesto al medir la longitud de onda de un láser de Helio-Neón estabilizado por metano, donde la asimetría de la línea del Kriptón conducía a diferentes resultados para la longitud de onda del láser en función del punto de la línea del Kriptón que se usase como referencia. En paralelo, comenzó a medirse la velocidad de propagación de la luz c combinando medidas independientes de frecuencia f y de longitud de onda λ (c = f λ) y de nuevo, se llegaba a valores diferentes para la velocidad de la luz en función del punto de la línea del Kriptón que se usara como referencia. Esta contradicción puso de manifiesto que la definición del metro carecía de la precisión necesaria e impulsó a la decimoséptima Conferencia General en 1983 a definir el metro como [CGPM]
“El metro es la longitud del trayecto recorrido por la luz en el vacío durante 1/299 792 458 segundos”
El metro ha sido desde el inicio una unidad pionera en basar su definición en cantidades cada vez más universales, constantes y fundamentales de la física. Ha ido siempre abriendo camino al resto de unidades que han ido reproduciendo el mismo modelo hasta culminar en la reciente revisión del SI donde todas las unidades están definidas a partir de constantes de la naturaleza.
5. El segundo
Resulta sorprendente que hasta 1956 no hubiera definición oficial del segundo. Era de dominio público que un segundo era simplemente la fracción 1/86400 de un día y el concepto de día se consideraba conocido por todos. Sin embargo, a partir de 1955, la invención y construcción de relojes atómicos supuso una revolución para la medida del tiempo. Se puso en evidencia, por ejemplo, que la duración de un día aumentaba en 1,7 milisegundos cada cien años. Ello condujo en primer lugar a cambiar la definición vigente por una que ligara el segundo a la duración de un año en particular, evitando así los problemas de variabilidad del día terrestre. La propuesta vino de los astrónomos. En 1956, el segundo fue definido como:
“El segundo es la fracción 1/ 31 556 925,9747 del año trópico 1900 enero 0 a las 12 horas de la efeméride”
Esta definición fue claramente concebida por astrónomos y fue difícilmente entendible fuera de esa comunidad. A pesar de ser promulgada, rápidamente engendró dos problemas: el primero era la inaccesibilidad de la definición por hacer referencia a un año tan lejano. El segundo era que, dado que el día solar medio aumentaba en 1,7 ms cada 100 años, y que esos desfases se acumulaban con el tiempo, sería necesario con el paso del tiempo añadir segundos intercalares a la definición para adaptar el año según la definición al año vigente. Por todo ello, finalmente, en 1967, el segundo atómico acabaría reemplazando a la definición astronómica. En unos pocos años, el avance espectacular de los relojes atómicos puso de manifiesto que la precisión que ofrecían iba a superar sin comparación posible a cualquier medida que viniera de observaciones astronómicas. En 1967 la 13ª Conferencia General decidió que [CGPM]
“Un segundo es la duración de 9 192 631 770 oscilaciones de la radiación emitida en la transición entre los dos niveles hiperfinos del estado fundamental del isótopo 133 del átomo de Cesio 133”
Esta definición sigue vigente en la actualidad, aunque la revisión del SI ha cambiado la redacción, siendo ahora:
“El segundo se define al fijar el valor numérico de la frecuencia de la transición hiperfina del estado fundamental no perturbado del átomo de cesio 133, ΔνCs, en 9 192 631 770, cuando se expresa en la unidad Hz, igual a s-1”
Se prevé una futura redefinición del segundo en torno al 2030 en la que se seleccionará una transición atómica óptica en lugar de una transición de microondas como la actual. Los relojes atómicos superan notablemente en repetibilidad ya desde hace varios años a los de Cesio. Una redefinición permitiría ganar dos órdenes de magnitud en la precisión de las medidas de tiempo y por extensión en la precisión del posicionamiento terrestre, que es la medida que está impulsando esta redefinición. La demora en redefinirlo se justifica porque los métodos de comparación de los relojes ópticos que están en diferentes continentes todavía no alcanzan un nivel suficiente de exactitud.
6. El amperio
Hacia finales del siglo XIX, la cuestión de los estándares eléctricos fue cada vez de mayor actualidad a causa de la veloz electrificación de la mayoría de aspectos de la producción industrial y también en la vida doméstica en general. A mediados del siglo XIX, la concepción general era que las unidades eléctricas absolutas debían estar basadas en comparaciones con cantidades medidas en unidades mecánicas de longitud, masa y tiempo. Sin embargo, hacia 1939, Giovanni Giorgi propuso un sistema de cuatro dimensiones, Metro, Kilogramo, Segundo (MKS) y una cuarta unidad eléctrica, a escoger. Tras la guerra, en 1946, el CIPM retomó el asunto y aprobó una resolución en la que se definían las unidades eléctricas amperio, voltio y ohmio. Estas definiciones entraron en vigor en 1948 y fueron aprobadas por la novena Conferencia General de 1948. La definición del amperio rezaba [CGPM]:
“El amperio es la corriente constante que, mantenida en dos conductores rectos paralelos de longitud infinita, de sección circular despreciable, y colocados a un metro de distancia en el vacío, produciría entre estos conductores una fuerza igual a 2 × 10-7 Newton por metro de longitud”.
En 1980, Klaus von Klitzing anunció su descubrimiento del efecto Hall cuántico. Este avance permitía vincular un patrón de resistencia directamente al cociente h/e2, donde h es la constante de Planck y e la carga eléctrica elemental. Este efecto, combinado con el efecto Josephson, descubierto por Brian Josephson en 1962, que abría el camino para vincular el patrón de tensión con el cociente 2e/h, conduciría a una pequeña revolución en la metrología eléctrica. Una de sus más notables consecuencias sería la posibilidad de vincular la masa con las constantes fundamentales a través de un experimento eléctrico-mecánico que sería concebido por Bryan Kibble en 1976 [Kibble 1976] y que sería conocido como balanza de potencia (watt balance) y más recientemente como balanza de Kibble, en honor a su inventor.
Las constantes de von Klitzing y de Josephson fueron llamadas respectivamente RK y KJ
\(R_{K}=\frac{h}{e^{2}}\) y \( K_{J}=\frac{2e}{h}\)
En 1988 el CIPM decidió adoptar valores convencionales para las constantes RK y KJ con el objetivo de basar una representación del ohmio y del voltio en estos efectos cuánticos [CIPM]. Estos valores convencionales fueron designados como RK-90 y KJ-90, y se les atribuyeron los valores RK-90=25 812,807 Ω y KJ-90=483 597,9 GHz/V, sin incertidumbre asociada. A partir de entonces, a pesar de que la unidad eléctrica básica era el amperio, la realización y la diseminación de las unidades eléctricas se basó en estos efectos cuánticos y los valores convencionales asociados [Taylor 1989]. Ello condujo al uso de un sistema de unidades eléctricas paralelo al SI, y por lo tanto fuera del SI, que no podía considerarse como satisfactorio.
Para permitir a la comunidad eléctrica volver plenamente al SI, la propuesta de redefinir el amperio fijando el valor numérico de la carga elemental e y de la constante de Planck h, se perfilaba como la solución de mayor conveniencia para la metrología eléctrica [CCEM MeP, CCEM note 2017]. De este modo, se podrían abandonar los valores convencionales RK-90 y KJ-90 y calcular directamente RK y KJ a partir de los valores fijados para h y e [Fletcher 2014] y basar la diseminación eléctrica en constantes fundamentales y no en valores convencionales.
Ello conllevaba como consecuencia la redefinición del kilogramo, que ocurre cuando se fija el valor numérico de la constante de Planck. Por ello, una redefinición conjunta del amperio y del kilogramo se reveló necesaria.
La determinación de la carga elemental e no necesitaba experimentos dedicados, ya que podía ser calculada a partir de los valores experimentales de la constante de estructura fina α y de la constante de Planck h usando la relación
\(\alpha=\frac{e^{2}c\mu_{0}}{2h}\)
teniendo en cuenta que la velocidad de la luz c y la permeabilidad magnética del vacío μ0=4π×10-7 tenían valores exactos antes de la revisión.
En 2018 la 26ª Conferencia General adoptó la siguiente definición del amperio [CGPM]:
“El amperio, símbolo A, es la unidad SI de intensidad de corriente eléctrica. Se define al fijar el valor numérico de la carga elemental, e, en 1,602 176 634 × 10-19, cuando se expresa en la unidad C, igual a A·s, donde el segundo se define en función de ΔνCs”
En el SI revisado μ0 ya no tiene un valor exacto y debe ser medida experimentalmente.
7. El kelvin
A diferencia del grado Celsius (históricamente conocido como grado centígrado) comúnmente usado en la vida cotidiana, el kelvin (K) es una medida absoluta de la temperatura. Esta escala fue introducida a mediados del siglo XIX y se basa en el hecho de que existe un límite inferior a toda temperatura, un cero absoluto. A diferencia del caso del grado Celsius, en el que el cero ha sido escogido arbitrariamente como la temperatura de fusión del hielo, el cero de la escala kelvin es un cero absoluto. La temperatura en Celsius t se expresa en función de la temperatura termodinámica (en Kelvin) T como:
t/°C = T/K – 273,15
Las variaciones de temperatura tienen el mismo valor numérico en ambas escalas.
La definición del kelvin como unidad de temperatura termodinámica tuvo lugar en 1954 en la 10ª CGPM, que seleccionó el punto triple del agua (punto en el que las tres fases, sólida, líquida y gaseosa coexisten) como un punto fijo fundamental al que se le asignó la temperatura de 273,16 K (equivalente a 0,01 °C). La 13ª CGPM (1967-1968) adoptó el nombre kelvin, con símbolo K, en lugar de “grado kelvin” con símbolo °K [CGPM].
Sin embargo, en la práctica la definición del kelvin se reveló poco precisa ya que la composición isotópica del agua utilizada afectaba a la temperatura de su punto triple. En 2005, el CIPM clarificó la definición precisando que la composición del agua debía ser la del agua oceánica media normalizada de Viena o VSMOW (Vienna Standard Mean Ocean Water) [CIPM]. Esta agua había sido definida en 1968 por la Agencia Internacional de la Energía Atómica (AIEA) y pretendía representar la composición isotópica media del agua terrestre: contiene exactamente 0,00015576 moles de 2H (deuterio) por mol de 1H (hidrógeno), 0,0003799 moles de 17O por mol de 16O y 0,00020052 moles de 18O por mol de 16O. El kelvin quedaba así definido respecto a un invariante (la temperatura del punto triple) pero de una sustancia específica con una composición isotópica particular. Las calibraciones de altas temperaturas sufrían por consecuencia al deberse comparar a una temperatura muy distante. La necesidad de una definición a partir de un invariante más fundamental se hacía sentir.
Las aportaciones de Maxwell y Boltzmann habían puesto de manifiesto que la temperatura también podía ser definida a nivel microscópico como una medida de la agitación de los constituyentes de la materia. En un cuerpo mantenido a temperatura T, la energía cinética media es proporcional a kT, en la que k es la constante de Boltzmann, que vincula la energía con la temperatura. La nueva propuesta sería entonces redefinir el kelvin fijando un valor numérico exacto de la constante de Boltzmann en lugar de la temperatura del punto triple del agua. Ello permitiría que la definición no siguiera dependiendo de una sustancia o experimento particular y garantizaría la perennidad de la unidad en el muy largo plazo, ya que la constante de Boltzmann es una constante física invariante en el tiempo y en el espacio. Esto permitiría además disminuir la incertidumbre en las calibraciones a muy bajas temperaturas (inferiores a 20 K) y a muy altas temperaturas (superiores a 1300 K) [Anhalt 2016].
Para asegurar la continuidad de la utilización del kelvin en caso de una redefinición, la constante de Boltzmann debía ser medida experimentalmente con una incertidumbre comparable a la de la realización del kelvin en vigor. Para ello el CIPM requirió la obtención de una incertidumbre relativa inferior a una parte por millón (10-6 en términos relativos) y que por lo menos dos determinaciones de k fueran obtenidas por métodos diferentes y con incertidumbres inferiores a 3·10– 6 [CCT 2017].
Uno de los métodos más exitosos para medir k ha sido el del llamado “termómetro acústico casi esférico” [Moldover 2014]. Su principio consiste en medir la velocidad de un gas situado dentro de un recinto casi esférico a la temperatura del punto triple del agua.
Tras más de una década de trabajos incesantes en 12 laboratorios repartidos en 8 países [Pitre 2017], en julio de 2017 la constante de Boltzmann era determinada con una incertidumbre de 0,37·10-6, con un valor de k = 1,38064903(51) ·10—23 J/K por el comité internacional CODATA TGFC (Task group on fundamental constants) [Newell 2018, Mohr 2018] (ver figura 1).
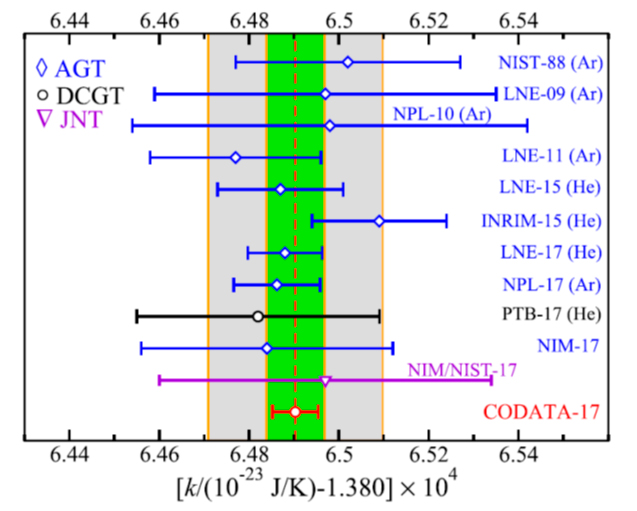
Ya se daban pues las condiciones para que la CGPM en 2018 definiera el kelvin como
“El kelvin, símbolo K, es la unidad de temperatura termodinámica. Se define al fijar el valor numérico de la constante de Boltzmann, k, en 1,380 649 × 10-23 cuando se expresa en la unidad J·K-1, igual a kg·m2·s-2·K-1 donde el kilogramo, el metro y el segundo se definen en función de h, c y ΔνCs”
Más allá de la redefinición, el impacto económico que se espera será importante ya que las mediciones de temperatura intervienen en el 80 % de los procesos industriales. Actualmente, en paralelo a la termometría primaria, existen escalas empíricas de temperatura con puntos fijos, principalmente ITS-90 (escala internacional de temperatura de 1990) [Preston-Thomas 1990]. Esta escala podrá seguir usándose, teniendo en cuenta que no se trata de un método primario [CCT Mep].
8. El mol
La razón por la que los químicos necesitan una unidad específica, el mol, es que los átomos y moléculas reaccionan uno por uno y no por peso o por masa. La magnitud que mide el número de partículas de una sustancia se designa cantidad de sustancia y representa una magnitud bien diferente a la masa. La propuesta de incluir el mol como unidad básica del SI se presentó por primera vez en la Conferencia General de 1967, que decidió rechazarla. Se elaboró una proposición más detallada en la siguiente Conferencia General de 1971, que finalmente fue adoptada con tres votos en contra. La definición escogida para el mol fue la siguiente [CGPM]:
“El mol es la cantidad de sustancia de un sistema que contiene tantas partículas elementales como átomos hay en 12 gramos de carbono-12”.
El número de átomos que hay en 12 gramos de Carbono 12 se conoce como número de Avogadro.
Esta definición ha sido de gran utilidad para la comunidad química. Sin embargo, en los últimos años, aprovechando que se estaba preparando una revisión del SI, la comunidad química propuso considerar una nueva definición del mol que lo desvinculara del kilogramo [Marquardt 2018]. De este modo, se reconocería la naturaleza estequiométrica de la química. Para ello se podría fijar un valor exacto del número de Avogadro y por consiguiente de la constante de Avogadro.
La 26ª Conferencia General de Pesas y Medidas adoptó en 2018 como nueva definición del mol la siguiente [CGPM]:
“El mol, símbolo mol, es la unidad SI de cantidad de sustancia. Un mol contiene exactamente 6,022 140 76 × 1023 entidades elementales. Esta cifra es el valor numérico fijo de la constante de Avogadro, NA, cuando se expresa en la unidad mol-1, y se denomina número de Avogadro.
La cantidad de sustancia, símbolo n, de un sistema, es una medida del número de entidades elementales especificadas. Una entidad elemental puede ser un átomo, una molécula, un ion, un electrón, o cualquier otra partícula o grupo especificado de partículas.”
9. La candela
La candela es la unidad de intensidad luminosa del SI, y sirve para medir la intensidad luminosa en una dirección particular emitida por una fuente luminosa. Sirve para medir la capacidad de iluminar de una fuente dada. Es la unidad básica de la fotometría. Reemplaza a una vieja unidad de medida, la vela o bujía que presentaba una intensidad luminosa aproximada de una candela. En 1948, la 9ª CGPM adoptó el nombre “candela” y símbolo “cd” y su definición fue basada en la intensidad luminosa de un radiador de Planck (un cuerpo negro) a la temperatura de congelación del platino, 2045 K. Esta definición fue ligeramente modificada en 1967.
En 1979, debido a las dificultades prácticas para realizar un radiador de Planck a temperaturas elevadas y gracias a las nuevas posibilidades abiertas por la radiometría, la 16ª CGPM adoptó una nueva definición de la candela, basada en la potencia óptica de una radiación [CGPM]:
“La candela es la intensidad luminosa, en una dirección dada, de una fuente que emite una radiación monocromática de frecuencia 540 × 1012 Hz y cuya intensidad energética en esa dirección es de 1/683 vatios por estereorradián”.
En 2018, la 26ª CGPM ha cambiado ligeramente la formulación de esta definición sin cambiar la definición [CGPM]:
“[La candela] se define al fijar el valor numérico de la eficacia luminosa de la radiación monocromática de frecuencia 540 × 1012 Hz, Kcd, en 683, cuando se expresa en la unidad lm·W-1, igual a cd·sr·W-1 o a cd·sr·kg-1·m-2·s3, donde el kilogramo, el metro y el segundo se definen en función de h, c y ΔνCs”.
10. El kilogramo
La redefinición del kilogramo es probablemente la más emblemática de la revisión del SI, acontecida en 2018. El kilogramo ha sido definido desde 1889 como la masa de un artefacto y, justo antes de la redefinición de 2018, era la única de las unidades del SI definida en función de un objeto material [Davis 2003].
En 1889 se estableció un sistema jerárquico entre el prototipo internacional del kilogramo (K), sus seis copias oficiales guardadas en el BIPM, con las que se le compararía periódicamente, y las más de ochenta copias distribuidas por todo el mundo que fueron calibradas en el BIPM al inicio y comparadas con K en diversas ocasiones posteriormente. Este sistema ha funcionado de forma satisfactoria durante todos estos años sin que ningún problema mayor haya sido constatado, que haya precipitado una redefinición.
Las razones del cambio son, sin embargo, diversas. En el actual siglo XXI, un sistema basado en el valor convencional atribuido a un artefacto, sin incertidumbre, no resulta aceptable por razones de principio. Sabemos que el prototipo internacional puede estar sujeto a variaciones de masa debido al desgaste que implica usarlo, así como a posibles contaminaciones que resistan al proceso de limpieza al que se somete al prototipo antes de toda calibración.
Desde 1889 se han llevado a cabo tres comparaciones de masa entre el prototipo internacional y sus seis copias oficiales, después de su fabricación, para evaluar la estabilidad de la masa del prototipo internacional (figura 2). Estas comparaciones se conocen como verificaciones periódicas. En las dos primeras, en 1946 y en 1991, se pudo constatar que las copias habían sufrido variaciones de masa respecto al prototipo internacional, con un valor medio de 30 microgramos (ver figura 1) [Girard 1993]. En la última verificación, en 2014, se encontró que las copias no habían variado prácticamente su masa con respecto a K desde la verificación precedente [Stock 2015, de Mirandés 2016]. Esto podría explicarse por las mejorías aportadas en 1991 a las condiciones de conservación de los prototipos.
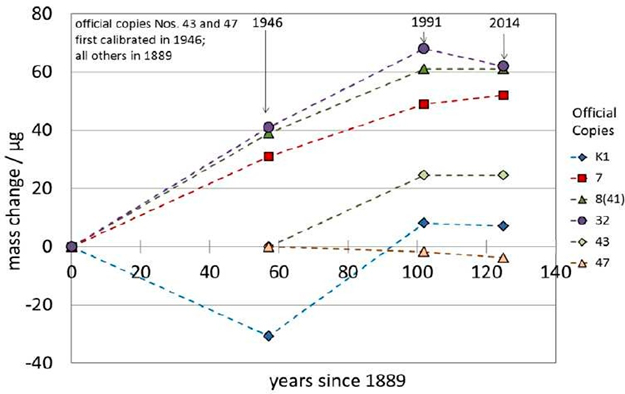
La intención de redefinir el kilogramo respecto a una constante fundamental de la naturaleza ha estado presente en el pensamiento de muchos científicos, desde Maxwell, quien así lo expresó en 1870 [Maxwell, 1870] hasta Jan de Boer (CIPM) quien en 1971 explicaba que una definición del kilogramo basada en la masa del protón le parecía natural, pero que una propuesta de esa naturaleza era de muy lejana aplicación ya que no se podía medir, en aquel entonces, con suficiente precisión la masa de las partículas atómicas.
El avance crucial que permitiría llevar a cabo tales perspectivas, fue el descubrimiento del efecto Hall cuántico por Klaus von Klitzing en 1980 [von Klitzing, 1980]. En aquel entonces, ya era comúnmente usado el efecto Josephson, descubierto en 1962 [Josephson, 1962], que permitía expresar la tensión de forma proporcional a fh/2e, donde h es la constante de Planck, e la carga elemental y f una frecuencia, pero resultaba insuficiente. El efecto Hall permitiría fabricar resistencias con valores proporcionales a h/e2. Estos efectos, conocidos con el nombre de efectos cuánticos macroscópicos, permitían establecer valores de tensión y resistencia al nivel de voltios y miles de ohmios. Ello contrastaba notablemente con las limitaciones que presentaban los efectos cuánticos anteriores que habían sido solo perceptibles en el dominio microscópico.
En 1975 Brian Kibble concibió la idea de usar una balanza de brazos iguales, a la que se llamó balanza de potencia, para comparar una potencia eléctrica con una potencia mecánica [Kibble 1976]. Combinándola con los efectos cuánticos macroscópicos, resultó posible usar la balanza de potencia para vincular el kilogramo con las constantes fundamentales, en particular con la constante de Planck, y esa posibilidad cambiaría el curso de la metrología de masa [Taylor 1991, Mills 2006].
El principio de la balanza de potencia, hoy llamada balanza de Kibble, es simple, pero su implementación práctica resulta muy compleja. Consta de dos fases, estática y dinámica, que se llevan a cabo separadamente. En la fase estática (figura 3) se suspende de un brazo de la balanza una pesa de masa m y de la otra una bobina de longitud L que se encuentra sumergida en un campo magnético radial B y por la que circula una corriente eléctrica I. La fuerza gravitacional mg ejercida por la pesa equilibra la fuerza electromagnética vertical que aparece en la bobina. En el equilibrio podemos escribir mg = ILB.
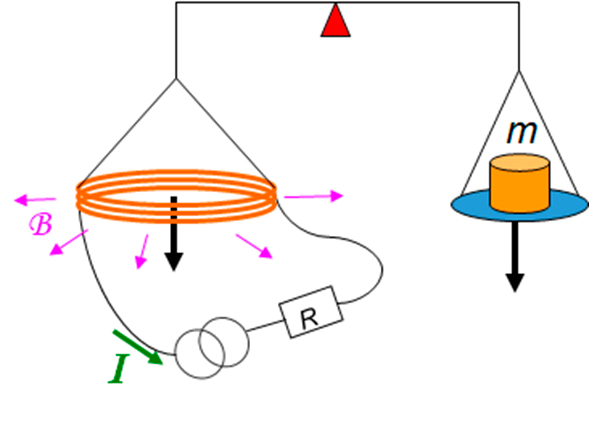
La fase estática presenta la limitación de que la medida precisa del campo magnético B y de la longitud de la bobina L es compleja. La brillante idea de Bryan Kibble para sortear esta dificultad fue incorporar una segunda fase, llamada fase dinámica (ver figura 4) en la que la bobina, esta vez sin corriente eléctrica, es desplazada verticalmente con velocidad constante v a través del mismo campo magnético B. En esas circunstancias, se genera una tensión U = BLv en los bornes de la bobina.
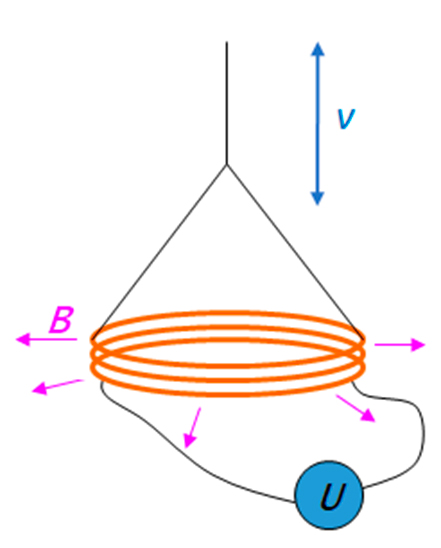
Combinando las ecuaciones de las fases estática y dinámica se puede escribir mgv = IU. Introduciendo los efectos cuánticos macroscópicos en las medidas de la tensión y la corriente se puede llegar a una relación entre la masa m y la constante de Planck h. Una de las complejidades del experimento es el alineamiento de los diferentes elementos y el logro de un desplazamiento puramente vertical de la bobina. Conseguir una medida de la constante de Planck con una balanza de Kibble con una incertidumbre relativa cercana a 2 × 10-8 suele llevar entre una y dos décadas de trabajo ininterrumpido.
Actualmente hay varias balanzas de Kibble en diferentes países del mundo [Haddad 2017, Robinson 2016, Thomas 2017, Wood 2017], algunas totalmente operacionales y otras en fase de desarrollo. La figura 5 muestra la balanza de Kibble del BIPM.

Un método alternativo para vincular la masa con la constante de Planck en un dominio diferente de la física ha sido el experimento llamado “de Avogadro”, también denominado método XRCD (X-ray crystal density) que consiste en medir el número de átomos contenidos en una esfera de 28Si mono-isotópico [Andreas 2011, Azuma 2015]. El diámetro de la esfera es medido por interferometría óptica clásica, y teniendo en cuenta que los átomos forman una estructura cristalina regular y que la distancia interatómica de la celda unidad de dicha estructura se puede medir de forma trazable al metro SI con un experimento que combina interferometría de rayos X e interferometría óptica, se puede deducir el número de átomos en la esfera. En este punto, simplemente pesando la esfera respecto al prototipo internacional se podría invertir la relación y redefinir la unidad de masa respecto a una constante fundamental, en este caso la masa del átomo de 28Si. En el sistema internacional este experimento puede ser también descrito como una manera de determinar la constante de Avogadro, NA, con unidad mol-1, que representa el vínculo entre la masa microscópica y macroscópica.
A pesar de que el principio del experimento es sencillo, su ejecución es compleja, y ello llevó al CIPM a establecer en 2002 un proyecto internacional, el proyecto Avogadro. Se invitó a participar a aquellos laboratorios nacionales trabajando en áreas relacionadas. El proyecto fue exitoso y reunió a laboratorios nacionales de países como Australia, Alemania, Italia, Japón, Reino Unido, Estados Unidos y el Instituto Europeo de Materiales de Referencia y Medidas (IRMM), así como el BIPM. Entre las diferentes partes del experimento, figuraban la producción de 28Si mono-isotópico, la medida del parámetro reticular del cristal, la fabricación de una esfera con esfericidad casi perfecta y la técnica para evaluar dicha esfericidad, estudios de la superficie y la oxidación de la esfera, medidas de su densidad, análisis de pureza, medidas de masa molar, medidas de las dimensiones de la esfera, de su masa, análisis de la perfección del cristal y evaluación de sus defectos. El objetivo fijado fue el de alcanzar una incertidumbre final de 2 partes en 108, el mismo fijado para las balanzas de Kibble [Fuji, 2016].
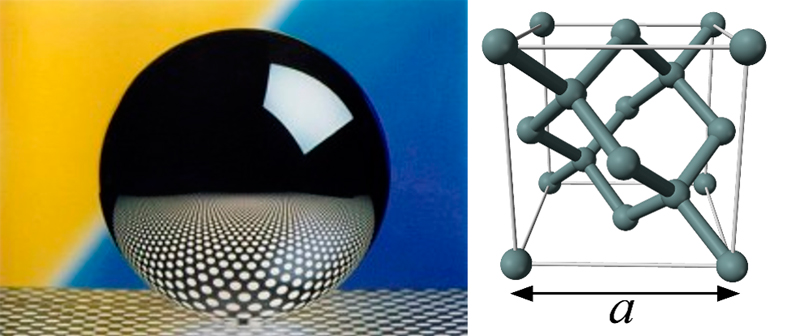
28Si. Derecha: celda unidad del Si, con una estructura cúbica de 8 átomos por celda unidad con parámetro reticular a La ecuación básica que vincula las cantidades medidas para determinar NA es:
NA=nM(Si)/(ρa3)
donde n es el número de átomos en la celda unidad, idealmente 8 si el cristal no tuviera defectos (ver figura 6); M(Si) es la masa molar del silicio; ρ es la densidad de la esfera y a el parámetro reticular.
Aunque las dos rutas posibles para redefinir el kilogramo son muy distintas, sus resultados pueden ser comparados utilizando ecuaciones físicas que relacionan la masa del átomo de silicio m(28Si), la constante de Avogadro NA, y la constante de Planck h, en particular la ecuación
NAh=[cα2/2R∞][MuAr(e)]
donde c es la velocidad de la luz en el vacío, α es la constante de estructura fina, la constante de Rydberg, Mu la constate de masa molar, que el en SI previo a la revisión valía exactamente 10-3 kg mol-1, y la masa atómica relativa del electrón. Mu y c eran exactas en el SI previo a la revisión, se conoce con una incertidumbre relativa de partes en 1012; Ar(e) se conoce en partes en 1010; la constante de estructura fina se conoce en partes en 1010; De este modo, la constante de Planck y la constante de Avogadro pueden deducirse la una de la otra con una incertidumbre relativa equivalente a la de la constante de estructura fina, que es de partes en 1010.
Han sido necesarios unos treinta años para que estos experimentos alcancen niveles de consistencia e incertidumbre suficientes para proceder a un cambio de definiciones del SI.
El comité consultivo de la masa, CCM, fijó en 2013 [CCM 2013] las condiciones estimadas como necesarias para proceder a una redefinición del kilogramo en función de la constante de Planck. En particular, requirió que al menos tres experimentos independientes, incluyendo ambos métodos de Kibble y Avogadro, obtuvieran medidas consistentes de la constante de Planck, con incertidumbres relativas inferiores a 5 partes en 108; al menos una de esas determinaciones debería tener una incertidumbre relativa inferior a 2 parte en 108. Estas condiciones se cumplieron en 2017 [Bartl 2017, Kuramoto 2017].
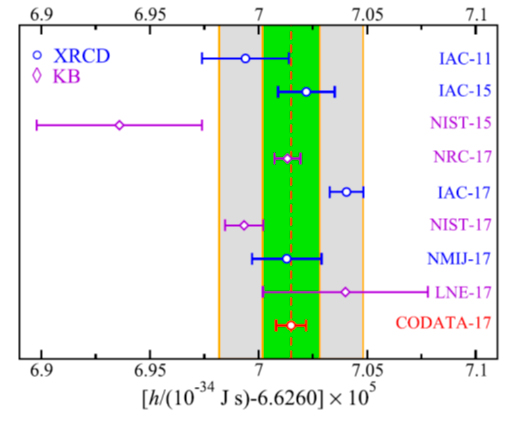
A mediados de 2017 el comité internacional CODATA TGFC realizó un ajuste por mínimos cuadrados de todas las medidas de h y NA disponibles hasta esa fecha, y que se muestran en la figura 7. El valor ajustado de h fue h = 6,626 070 150(69) × 10-34 J·s con una incertidumbre relativa de 1,0 × 10-8 [Newell 2018, Mohr 2018]. Esta incertidumbre satisfizo al CCM para recomendar al CIPM [CCM 2017] que presentara a la Conferencia General de 2018 el proyecto de redefinición del kilogramo fijando el valor numérico de la constante de Planck.
Sin embargo, el CCM también notó que las tres medidas de h más precisas, designadas por NRC-17, IAC-17 y NIST-17 en la figura 7, no presentaban un recubrimiento óptimo entre ellas. Para evitar que ello se tradujera en diferencias significativas en la diseminación ulterior del kilogramo, después de la redefinición [CCM MeP-kg], se convino que tras la revisión del SI se adoptaría temporalmente un valor de consenso para el kilogramo y que todas las diseminaciones de la unidad de masa se harían a partir de dicho valor. Esta es la estrategia que se seguirá hasta que el acuerdo entre las mejores realizaciones primarias sea suficientemente bueno como para que diseminaciones independientes a partir de cada una de ellas sean perfectamente consistentes. En ese punto el valor de consenso ya no será necesario y se eliminará.
Con esas precauciones, la conferencia General de Pesas y Medidas adoptó en 2018 una nueva definición del kilogramo, que reza [CGPM]:
El kilogramo, símbolo kg, es la unidad SI de masa. Se define al fijar el valor numérico de la constante de Planck, h, en 6,626 070 15 × 10-34, cuando se expresa en la unidad J·s, igual a kg·m2·s-1, donde el metro y el segundo se definen en función de c y ΔνCs
11. Síntesis de la revisión del SI
A partir de su revisión, el SI es el sistema de unidades en el que:
La frecuencia de la transición hiperfina del estado fundamental no perturbado del átomo de cesio 133, ΔνCs, es 9 192 631 770 Hz
La velocidad de la luz en el vacío, c, es 299 792 458 m/s
La constante de Planck, h, es 6,626 070 15 × 10-34 J·s
La carga elemental, e, es 1,602 176 634 × 10-19 C
La constante de Boltzmann, k, es 1,380 649 × 10-23 J/K
La constante de Avogadro, NA, es 6,022 140 76 × 1023 mol-1
La eficacia luminosa de la radiación monocromática de frecuencia 540 × 1012 Hz, Kcd, es 683 lm/W
con los anteriores valores numéricos carentes de incertidumbre y donde las unidades hercio, julio, culombio, lumen y vatio, con símbolos Hz, J, C, lm y W respectivamente, están relacionadas con las unidades segundo, metro, kilogramo, amperio, kelvin, mol y candela, con símbolos s, m, kg, A, K, mol y cd respectivamente, por las expresiones Hz = s–1, J = m2 kg s–2, C = A s, lm = cd m2 m–2 = cd sr y W = m2 kg s–3.
Una profusa explicación de esta revisión puede encontrarse en el folleto explicativo del SI, llamado “Brochure du SI” [SI Brochure], editado por el BIPM. Allí se encuentran asimismo los textos oficiales de las resoluciones adoptadas por la Conferencia General desde 1889 hasta nuestros días y que conforman la doctrina central del SI.
Notamos en particular que la definición central del SI revisado no comporta una definición explícita de las unidades básicas, como era el caso en precedentes versiones, sino una especificación del valor numérico exacto de siete constantes fundamentales de la naturaleza. Ello define implícitamente las unidades del sistema, sin establecer una jerarquía entre unidades básicas y unidades derivadas. La distinción entre esas dos clases de unidades será mantenida por razones históricas y pedagógicas, pero no constituye una característica esencial de la revisión.
Los valores numéricos escogidos para esas constantes garantizan la continuidad entre las anteriores unidades y las unidades redefinidas, de forma que el usuario final no perciba ningún cambio en la vida cotidiana. Sólo los laboratorios trabajando con alta precisión notarán algún cambio, en particular en el área eléctrica y de masa. Para ello ha sido necesario medir dichas constantes en el sistema precedente con gran precisión antes de proceder al cambio.
En el SI sólo siete cantidades pueden tener valores numéricos exactos en un momento dado. Las cuatro constantes h, NA, k y e, quedarán fijadas por primera vez y ello implicará que cuatro cantidades que hasta ahora tenían valores exactos serán de nuevo libres y deberán determinarse a partir de medidas experimentales, con una incertidumbre asociada a sus valores. Estas cuatro cantidades son la masa de K, la masa molar del carbono-12, la temperatura del punto triple del agua Ttpw y la constante de permeabilidad magnética del vacío µ0.
12. Epílogo. El SI revisado y el futuro rol del BIPM
La estructura del Tratado del Metro de 1875 ha resistido impecablemente el paso del tiempo y ha establecido una estructura metrológica internacional que ha permitido construir un sistema de unidades capaz de adaptarse al paso del tiempo sin perder sus características esenciales.
Durante este tiempo el BIPM ha sabido propiciar la colaboración de especialistas en los diferentes dominios metrológicos y coordinar los resultados de sus interacciones, así como conservar y fabricar prototipos y patrones internacionales. Para realizar con éxito esas tareas el BIPM ha sabido mantener su neutralidad y asumir un carácter internacional. Estas características continuarán siendo indispensables para que el BIPM siga desarrollando sus funciones en el contexto del SI revisado.
En este nuevo marco, el BIPM seguirá siendo clave en la garantía de la uniformidad mundial de las unidades de medida y su diseminación. Para ello serán esenciales las comparaciones claves entre todos los laboratorios nacionales que se llevan a cabo en el marco del CIPM MRA (Mutual Recognition Arrangement) [MRA 1999]. La decisión sobre la naturaleza y la periodicidad de las comparaciones clave reposa sobre los comités consultivos del CIPM. En este contexto, el BIPM continuará ejerciendo el rol de coordinador de la metrología mundial.
Respecto al futuro cercano del sistema internacional, una redefinición del segundo en función de una frecuencia óptica podría ocurrir en los próximos diez años. Los mejores relojes atómicos ópticos ya superan en repetibilidad a los relojes atómicos actuales basados en la transición de microondas del átomo de Cesio. Técnicamente el desafío que se debe asumir antes de poder redefinir el segundo es el de comparar con precisión relojes atómicos ópticos de diferentes continentes. La investigación en este campo es muy activa.
Referencias
Adler, K. 2003 The measure of all things: the seven-year odyssey and hidden error that transformed the world. Free Press. ISBN: 0743216768
Andreas B et al 2011 Counting the atoms in a 28Si crystal for a new kilogram definition Metrologia 48 S1–13
Anhalt K and Machin G 2016 Thermodynamic temperature by primary thermometry Phil. Trans. R. Soc. A 374 20150041
Azuma Y et al 2015 Improved measurement results for the Avogadro constant using a 28Si-enriched crystal Metrologia 52 360–75
Bartl G et al 2017 A new 28Si single crystal: counting the atoms for the new kilogram definition Metrologia 54 693–715
CCEM MeP-A Mise en pratique for the definition of the ampere and other electrical units in the SI, available in Appendix 2 of the 9th edition of the SI brochure on the BIPM web site: www. bipm.org
CCEM note 2017 Guidelines for implementation of the ‘Revised SI’ available on the BIPM web site: www.bipm.org
CCM 2013 Report of the 14th meeting of the CCM Recommendation G1 (2013) of the CCM submitted to the CIPM, On a new definition of the kilogram, page 36 http://www.bipm.org/utils/common/pdf/CC/CCM/CCM14.pdf
CCM 2017 Report of the 16th meeting of the CCM, Recommendation G1 (2017) of the CCM submitted to the CIPM, For a new definition of the kilogram in 2018, page 25 http://www.bipm.org/utils/common/pdf/CC/CCM/CCM16.pdf
CCM MeP-kg CCM, Mise en pratique for the definition of the kilogram in the SI, available in Appendix 2 of the 9th edition of the SI brochure on the BIPM web site: www.bipm.org
CCT MeP-K CCT, Mise en pratique for the definition of the kelvin in the SI, available in Appendix 2 of the 9th edition of the SI brochure on the BIPM web site: www.bipm.org
CCT 2017 Report of the 28th meeting of the CCT, Recommendation T1 (2017) of the CCT submitted to the CIPM, For a new definition of the kelvin in 2018, page 26 https://www.bipm.org/utils/common/pdf/CC/CCT/CCT28.pdf
CIPM decisions, https://www.bipm.org/en/committees/cipm/meeting/106.html
CGPM resolutions, https://www.bipm.org/en/worldwide-metrology/cgpm/resolutions.html
Davis R 2003 The SI unit of mass Metrologia 40 299–305
de Mirandés E, Barat P, Stock M and Milton M 2016 Calibration campaign against the international prototype of the kilogram in anticipation of the redefinition of the kilogram part II: evolution of the BIPM as-maintained mass unit from the 3rd Periodic Verification to 2014 Metrologia 53 1204–14
Fletcher N, Rietveld G, Olthoff J, Budovsky I and Milton M 2014 Electrical units in the new SI: saying goodbye to the 1990 values NCSLI Measure J. Meas. Sci. 9 30–5
Fujii K et al 2016 Realization of the kilogram by the XRCD method Metrologia 53 A19–45
Girard G. 1993 La troisième verification périodique des prototypes nationaux du kilogramme. Procès Verbaux du Comité International des poids et mesures. https://www.bipm.org/utils/common/pdf/3eVerificationkg-FR.pdf
Haddad D et al 2017 Measurement of the Planck constant at the National Institute of Standards and Technology from 2015 to 2017 Metrologia 54 633–41
Josephson B D 1962 Possible new effects in superconductive tunnelling Physics Letters 1, 7, 251-253
Kibble B P 1976 A measurement of the gyromagnetic ratio of the proton by the strong field method Atomic Masses and Fundamental Constants vol 5 ed J H Sanders and A H Wapstra (New York: Plenum) pp 545–51
Kuramoto N et al 2017 Determination of the Avogadro constant by the XRCD method using a 28Si-enriched sphere Metrologia 54 716–29
Marquardt R et al 2018 Definition of the mole (IUPAC Recommendation 2017) Pure Appl. Chem. 90 175–80
Maxwell J C 1870 Report of the 40th Meeting of the British Association for the Advancement of Science Notes and Abstracts of Misc. Comm., Mathematics and Physics, pp 1–9
Mills I M, Mohr P J, Quinn T J, Taylor B N and Williams E R 2006 Redefinition of the ampere, kelvin and mole: a proposed approach to implementing CIPM recommendation 1 (CI-2005) Metrologia 43 227–46
Mohr P J, Newell D B, Taylor B N and Tiesinga E 2018 Data and analysis for the CODATA 2017 special fundamental constants adjustment Metrologia 55 125–46
Moldover M R et al 2014 Acoustic gas thermometry Metrologia 51 R1–19
MRA 1999 Mutual recognition of national measurement standards and of calibration and measurement certificates issued by national metrology institutes (BIPM) www.bipm.org/utils/en/ pdf/CIPM-MRA-2003.pdf
Newell D B et al 2018 The CODATA 2017 values of h, e, k, and NA for the revision of the SI Metrologia 55 L13–16
Pitre L et al 2017 New measurement of the Boltzmann constant k by acoustic thermometry of helium-4 gas Metrologia 54 856–73
Preston-Thomas H 1990 The international temperature scale of 1990 (ITS-90) Metrologia 27 3–10
Quinn, T. J. 2011 From artefacts to atoms, Oxfortd University Press. ISBN: 9780195307863
Robinson I A and Schlamminger S 2016 The watt or Kibble balance: a technique for implementing the new SI definition of the unit of mass Metrologia 53 A46–74
SI Brochure 9th edition of the SI Brochure, available on the BIPM web page: www.bipm.org
Stock M, Barat P, Davis R S, Picard A and Milton M J T 2015 Calibration campaign against the international prototype of the kilogram in anticipation of the redefinition of the kilogram part I: comparisons of the international prototype with its official copies Metrologia 52 310–16
Stock M, Davis R, de Mirandes E and Milton M J T 2019, The revision of the SI- the result of three decades of progress in metrology Metrologia 56 022001
Taylor B N and Witt T J 1989 New international electrical reference standards based on the Josephson and quantum Hall effects Metrologia 26 47–62
Taylor B N 1991 The possible role of the fundamental constants in replacing the kilogram IEEE Trans. Instrum. Meas. 40 86–91
Thomas M et al 2017 A determination of the Planck constant using the LNE Kibble balance in air Metrologia 54 468–80
Von Klitzing K et al 1980 New Method for High-Accuracy Determination of the Fine-Structure Constant Based on Quantized Hall Resistance Phys. Rev. Lett. 45, 494
Wood B M, Sanchez C A, Green R G and Liard J O 2017 A summary of the Planck constant determinations using the NRC Kibble balance Metrologia 54 399–409









Comentarios