Pablo Santafé-Gabarda, Alejandro Ferrero, Néstor Tejedor y Joaquín Campos
Instituto de Óptica “Daza de Valdés”
Agencia Estatal CSIC, Madrid
RESUMEN
La BSSRDF (Bidirectional Scattering-Surface Reflectance Distribution Function) es una función que describe la variación de la radiancia de las áreas elementales de la superficie de un objeto respecto al flujo radiante direccionalmente incidente en esa superficie. Las medidas de esta función son muy útiles para caracterizar la translucidez de un objeto y para obtener las propiedades ópticas que afectan al esparcimiento o scattering en volumen. Sin embargo, a día de hoy no existen medidas de esta función con trazabilidad al Sistema Internacional de Unidades (SI) y, por lo tanto, no se ha definido ninguna escala de medida de esta función. Por este motivo, en el Instituto de Óptica “Daza de Valdés” (IO-CSIC) se ha desarrollado un sistema capaz de medir la BSSRDF de muestras translúcidas homogéneas y expresarla en unidades del SI.
ABSTRACT
The Bidirectional Scattering-Surface Reflectance Distribution Function (BSSRDF) describes the variation of the radiance from the elementary areas on the surface of an object with respect to the directionally incident radiant flux on that surface. Measurements of this function are very useful for characterizing the translucency of an object and for obtaining those optical parameters affecting volume scattering. However, to date there are no measurements of this function with traceability to the International System of Units (SI) and, therefore, no measurement scale has been defined for this function. Due to this, a system capable to provide SI-traceable measurements of the BSSRDF of homogeneous and translucent samples has been developed in the Instituto de Óptica “Daza de Valdés” (IO-CSIC).
PALABRAS CLAVES
Scattering sub-superficial, translucidez, escala de medida, BSSRDF.
KEYWORDS
Sub-surface scattering, translucency, measurement scale, BSSRDF.
1. Introducción
La BSSRDF (Bidirectional Scattering-Surface Reflectance Distribution Function) es una función que describe la variación de la radiancia de las áreas elementales de la superficie de un objeto respecto al flujo radiante que ha incidido direccionalmente en esa superficie. Por lo tanto, esta función está íntimamente ligada a las propiedades ópticas que afectan al scattering sub-superficial y a la translucidez del objeto. Matemáticamente se expresa como:
\(f_{ssr}\left (x_{i},r_{i};x_{r},r_{r} \right )=\frac{dL_{r}\left (x_{i},r_{i};x_{r},r_{r} \right )}{d\phi_{i}\left ( x_{i}, r_{i} \right ) }\)
(1)
donde \(f_{ssr}\) simboliza la BSSRDF y \(dL_{r}\) es el elemento diferencial de la radiancia emergente desde la posición \(x_{r}\) sobre la superficie del objeto en la dirección \(r_{r}\), generada por el elemento diferencial del flujo radiante, \(d\mathrm{\Phi}_i\), que ha incidido en la posición \(x_{i}\) de la misma superficie y en la dirección \(r_{i}\). Aunque se haya omitido, esta función también tiene una dependencia espectral en función del material.
La BSSRDF fue introducida en 1977 por F. Nicodemus et. al. [1] y es una particularización de la función general de scattering [2], \(S\left(x_i,r_i,\lambda_i,t_i;x_r,r_r,\lambda_r,t_r;L_i\right)\). Junto con la BSSRDF, se define también otra función de distribución de reflectancia más simple, la BRDF (Bidirectional Reflectance Distribution Function), la cual describe la distribución angular de la radiancia de una superficie respecto a la irradiancia recibida. Generalmente, la BRDF se ha utilizado para caracterizar la reflectancia de materiales opacos, es decir, materiales con una contribución del scattering sub-superficial despreciable. En la literatura se pueden encontrar diferentes sistemas desarrollados para realizar medidas de la BRDF con trazabilidad al Sistema Internacional de Unidades (SI) [6-8], así como comparaciones entre distintos laboratorios de sus escalas de medida de esta función [7].
En las últimas décadas se han desarrollado algunos sistemas de medida de la BSSRDF, ya que muchos laboratorios y grupos de investigación del sector de la computación gráfica necesitan probar sus modelos de reproducción virtual de objetos translúcidos con medidas reales [8-13]. Sin embargo, ninguno de estos sistemas es capaz de proporcionar medidas trazables al SI. La aparición a lo largo de los últimos años de nuevos modelos basados en el aprendizaje automático o machine learning ha aumentado la necesidad de disponer de medidas de la BSSRDF con trazabilidad al SI, ya que estos modelos exigen enormes cantidades de datos para entrenarse, y estos datos deben poder referenciarse al mismo sistema de unidades [14].
Uno de los motivos de que no exista todavía un sistema capaz de realizar medidas trazables de la BSSRDF al SI es que la medida de la esta función es un proceso complicado, que requiere de un sistema de medida complejo. Para realizar una medida completa de la BSSRDF, es decir, en cualquier posición de iluminación y colección sobre la superficie de una muestra y a cualquier dirección de iluminación y colección, es necesario un sistema de medida con 8 grados de libertad (2 para cada posición y 2 para cada dirección). En el caso de muestras homogéneas, las posiciones de iluminación y colección se pueden reducir a una posición de colección relativa a la posición de iluminación, que actúa como origen de coordenadas (véase Figura 1).
Cuando se realiza una medida de la BSSRDF, se deben realizar una serie de aproximaciones, ya que los elementos diferenciales de radiancia y flujo radiante incidente que aparecen en la definición teórica de la función no son físicamente medibles en el laboratorio. En su lugar, se mide el flujo radiante que ha incidido en la superficie de la muestra dentro del área irradiada, Ai, con un ángulo sólido de irradiación, i, “suficientemente estrecho” y la radiancia emergente desde el área de colección, Ar, dentro de un ángulo sólido de colección, r, “suficientemente estrecho”. El término “suficientemente estrecho” significa que la magnitud medida no varía dentro del ángulo sólido escogido y las áreas Ai y Ar deben ser lo más pequeñas posible para caracterizar correctamente la distribución espacial de la radiancia producida por el scattering sub-superficial.
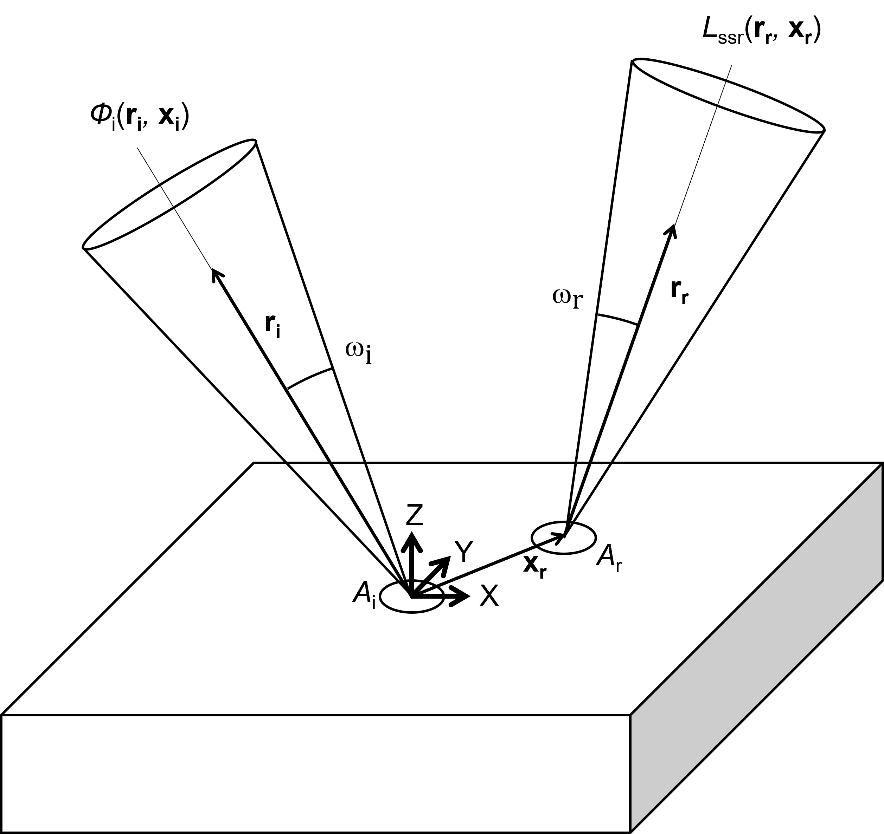
Los parámetros geométricos de un sistema de medida de la BSSRDF dependen del diseño del sistema, el cual está determinado por distintas decisiones tomadas para satisfacer tanto necesidades científicas (parámetros de medida, trazabilidad, etc.) como técnicas (tiempo de medida, coste, tamaño del sistema, etc.). En el Instituto de Óptica “Daza de Valdés” del CSIC (IO-CSIC) se ha desarrollado un sistema capaz de realizar medidas de la BSSRDF con trazabilidad al SI, basado en un sistema anterior desarrollado para realizar medidas de la BRDF [6], [15]. Se espera que este sistema sirva para establecer la primera escala de medida de la BSSRDF para transferir a otros laboratorios con instrumentos de medida más simples.
2. Sistema de medida
El sistema de medida desarrollado en el IO-CSIC se describe en la literatura [16] y consiste en un gonio-espectrofotómetro compuesto por tres subsistemas: un subsistema de iluminación fijo con resolución espectral, un subsistema de posicionamiento de la muestra con 6 grados de libertad de movimiento y un subsistema de detección con alta resolución espacial que puede moverse alrededor de la muestra en una dimensión. Con todo en conjunto, este sistema permite iluminar las muestras en cualquier dirección y con cualquier longitud de onda del rango visible, y detectar la distribución espacial de la radiancia en su superficie en cualquier dirección, independientemente de la dirección de iluminación. En la Figura 2 se representa un esquema del sistema.
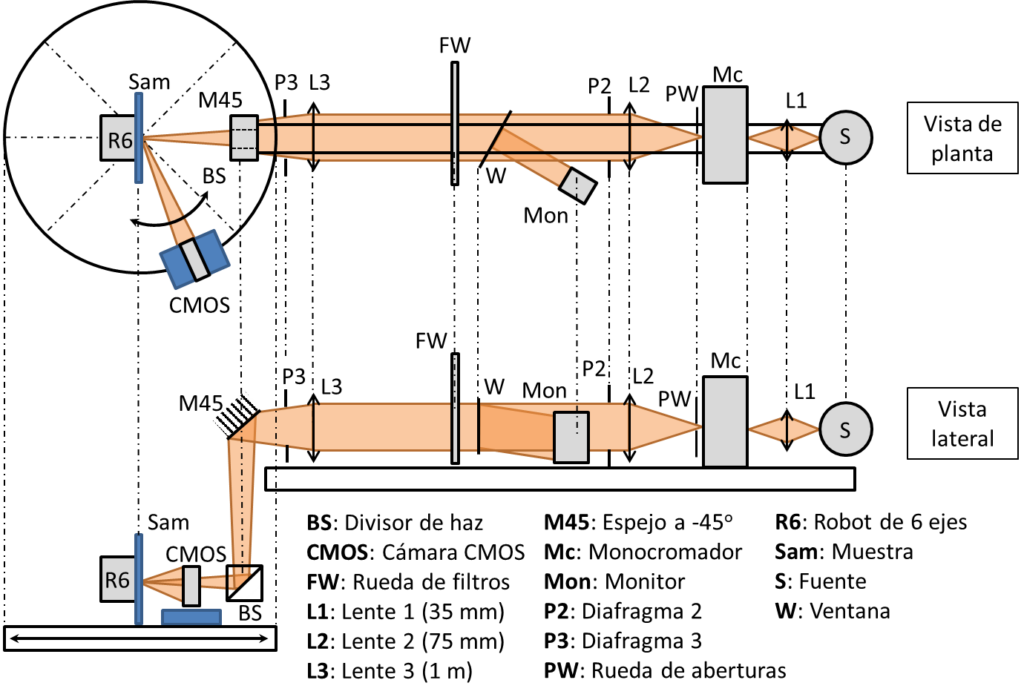
El sistema cuenta con una fuente de luz controlada por láser (LDLS, de sus siglas en inglés), basada en una lámpara de Xe, y un monocromador que le proporciona la resolución espectral en la medida de la BSSRDF. Justo a la salida del monocromador se coloca una rueda de aberturas, con diámetros desde 25 micrómetros hasta 2 milímetros, que permite variar el área irradiada sobre la superficie de la muestra. Mediante un sistema óptico compuesto por dos lentes se obtiene una imagen de la abertura seleccionada sobre el plano de la muestra, con un aumento aproximado de 4x. Entre las lentes el haz está prácticamente colimado y en él se sitúa una ventana de vidrio que refleja una pequeña porción del flujo radiante que en ella incide hacia un fotodetector, que monitoriza la estabilidad de la señal, y una rueda de filtros, con 3 filtros de densidad neutra de distintas transmitancias, una posición sin filtro y otra con un filtro opaco, que permite reducir la irradiancia sobre el plano de la muestra o bloquear por completo el haz incidente. Por último, un sistema periscópico formado por un espejo orientado a – 45° y un divisor de haz orientado a 45° respecto al eje óptico del sistema permite realizar medidas de retrorreflexión, es decir, detectar la radiancia en la misma dirección en que se ha realizado la incidencia.
El posicionamiento de la muestra en el sistema se realiza a través de un brazo robot de 6 ejes que puede orientar la muestra en cualquier dirección respecto al haz incidente de manera rápida y precisa. Por otro lado, la detección se realiza con una cámara CMOS (Complementary Metal-Oxide-Semiconductor) de alta sensibilidad. La cámara está montada sobre una plataforma que puede desplazarse alrededor de la muestra a través de un rail circular, de manera que, junto con el movimiento del brazo robótico, se puede realizar la observación desde cualquier dirección, dentro del hemisferio superior del plano de la muestra, independientemente de la dirección de iluminación. Las adquisiciones realizadas con la cámara son imágenes de alto rango dinámico, ya que es necesario resolver escenas con niveles de radiancia muy diferentes, lo cual añade dificultad a la trazabilidad de las medidas.
3. Modelo de medida
Para poder medir la BSSRDF es conveniente expresarla en términos de variables fácilmente medibles en el laboratorio. La ecuación (1) expresa la BSSRDF como la radiancia emergente desde el área de colección, \(A_{r}\), sobre la superficie de la muestra dentro del ángulo sólido de colección, \(\omega_{r}\), dividida entre el flujo radiante incidente, \(\mathrm{\Phi}_{i}\). La radiancia se puede expresar en términos de flujo reflejado, \(\mathrm{\Phi}_{r}\), a través de la siguiente expresión [17]:
\(L_{r}\left(x_{i},r_{i};x_{r},r_{r}\right)=\frac{\mathrm{\Phi}_{r}\left(x_{i},r_{i};x_{r},r_{r}\right)}{A_{p}\omega_{r}}\)
(2)
donde \(A_{p}\) es el área aparente del elemento superficial de radiancia, que en nuestro sistema queda definida por el área del campo de visión de un píxel de la cámara, \(A_{fov}\), y se define como el área real de dicho elemento (\(A_{r}\)) multiplicada por el coseno del ángulo que forma la dirección de colección con la dirección normal (perpendicular) a la superficie. De esta forma, la BSSRDF se puede expresar como un cociente entre el flujo radiante reflejado y el flujo radiante incidente multiplicado por un factor geométrico:
\(f {ssr}\left ( x{i},r_{i};x_{r},r_{r} \right ) = \frac{1}{A_{fov} \omega_r}\frac{\mathrm{\Phi}r\left(x{i},r_{i};x_{r},r_{r}\right)}{\mathrm{\Phi}i\left(x{i},r_{i}\right)}\)
(3)
La respuesta de los píxeles de la cámara, \(N\) (cuentas), está directamente relacionada con el flujo radiante que en ellos ha incidido, a través de la siguiente expresión:
\(N=\frac{\lambda}{hc}K\tau\eta_{e}t_{exp}\mathrm{\Phi}\)
(4)
donde el factor \(\frac{\lambda}{hc}\) (siendo \(h\) la constante de Planck y \(c\) la velocidad de la luz en el vacío) representa la inversa de la energía de un fotón de longitud de onda \(\lambda\) , \(K\) es el factor de conversión entre fotoelectrones y cuentas, \(\tau\) es la transmitancia de la lente de la cámara, \(\eta_{e}\) la eficiencia cuántica externa del píxel y \(t_{exp}\) es el tiempo de exposición. Para tomar imágenes de alto rango dinámico, se realizan una serie de adquisiciones a distintos tiempos de exposición que, posteriormente, se combinan para obtener una imagen en la que, en función de la radiancia, los distintos píxeles han empleado tiempos de exposición distintos. En esta imagen se divide la señal de cada píxel entre el tiempo de exposición empleado, obteniendo así una señal N’ (cuentas/s).
Finalmente, se obtiene una fórmula para el cálculo de la BSSRDF asociada a cada uno de los píxeles de la cámara cuyas variables son magnitudes medibles mediante los instrumentos del laboratorio:
\(f_{ssr,k} = \frac{\tau_{nd}}{A_{fov}\omega_{r}}\frac{N’_{r,k}}{\sum_{k}{N’_{i,k}}}\left\{C_{n} \right\}\)
(5)
donde \(f_{ssr,k}\) representa el valor de la BSSRDF del área elemental sobre la superficie de la muestra que corresponde al píxel “\(k\)”, \(\tau_{nd}\) es la transmitancia del filtro de densidad neutra empleado en la adquisición del flujo radiante incidente para evitar la saturación de la señal de los píxeles de la cámara, \(N’_{r,k}\) es la señal en unidades de cuentas·\(s^{-1}\) del píxel “\(k\)” en la adquisición de la radiancia sobre la superficie de la muestra, \(\sum_{k}{N’_{i,k}}\) es la suma de las señales de todos los píxeles, en unidades de cuentas·\(s^{-1}\), en la adquisición del flujo radiante incidente y \(C_{n}\) representa el conjunto de factores de corrección asociados a la detección (por ejemplo, el factor de corrección de la linealidad de la cámara, de su uniformidad, del cociente de responsividades, etc.).
Junto con el modelo de medida, viene asociado un análisis de todas las fuentes de incertidumbre presentes en la medida de la BSSRDF. Todas ellas están contempladas en la ecuación (5) a través de las propias variables relacionadas con la definición de la función o de los factores de corrección. De esta forma, asumiendo que no hay correlaciones entre las variables de entrada, la incertidumbre relativa de la medida de la BSSRDF se puede calcular como la raíz cuadrada de la suma cuadrática de las incertidumbres relativas de todos los elementos presentes en la ecuación de medida [18]. El sistema desarrollado en el IO-CSIC proporciona medidas de la BSSRDF con incertidumbres relativas con un intervalo de confianza del 95 % inferiores al 5 % para valores superiores a 102 sr·m-2.
4. Realización de la escala
Para realizar una escala de medida es necesario medir muestras estables que puedan ser reproducibles con cantidades de magnitud diferentes, para que otros laboratorios, posteriormente, puedan usar las mismas muestras para calibrar sus sistemas. En este caso, se han utilizado una serie de muestras translúcidas con valores controlados del tamaño medio de las partículas difusoras y su concentración, las cuales presentan niveles de translucidez diferentes. Estas muestras han sido manufacturadas por la empresa Covestro Deutschland AG dentro del proyecto europeo BxDiff: New quantities for the measurement of appearance, que ha sido financiado por el programa EMPIR (European Metrology Programme for Innovation and Research). En un trabajo anterior [16] se midió la BSSRDF de las 12 muestras suministradas con la finalidad de evaluar el sistema de medida. Los resultados de este trabajo permitían clasificar todas las muestras en tres grupos según su distribución espacial de BSSRDF. Por lo tanto, se ha decidido escoger una muestra representativa de cada grupo para definir la escala de BSSRDF, las cuales se muestran en la Figura 3.
Aparte de las distintas muestras, para definir una escala de medida es necesario también establecer una serie de configuraciones y parámetros de medida para las variables que influyen en el valor de la magnitud; esto es, geometrías de medida, longitudes de onda, polarización, etc. En este trabajo se han propuesto tres geometrías de medida diferentes (véase Figura 4), una longitud de onda de iluminación de 550 nm y luz no polarizada. Las geometrías de medida seleccionadas son geometrías “en plano de incidencia”, es decir, que las direcciones de iluminación y colección se encuentran en el mismo plano perpendicular a la superficie de la muestra. El motivo de esta elección radica en la dificultad de algunos sistemas para realizar medidas en geometrías “fuera de plano de incidencia”. Además, las geometrías 1 y 2, que son recíprocas, son las que se suelen usar como estándar en caracterización de materiales, y la geometría 3 es típica en estudios de propiedades multiángulo de materiales.


En la Figura 5 se representan los resultados de la medida de la BSSRDF de las tres muestras seleccionadas para definir la escala con cada una de las geometrías propuestas. Se representan únicamente los valores de las posiciones que se encuentran en el plano de incidencia.
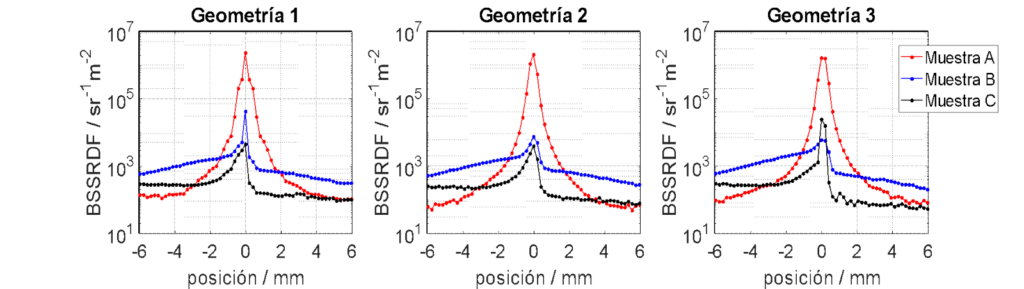
Como se puede observar en la Figura 3, las muestras A y C presentan una apariencia opaca y casi transparente, respectivamente, y la muestra B presenta una apariencia intermedia entre estos dos extremos. Traducido a la BSSRDF, se observa en la Figura 5 que la muestra de apariencia opaca (muestra A) presenta una curva muy picuda, con un valor máximo muy elevado en el centro del área irradiada y una disminución abrupta al alejarse del mismo. La muestra B, sin embargo, presenta una curva con una pendiente mucho más suave, síntoma del esparcimiento de la luz por toda su superficie. Por último, la muestra de apariencia más transparente simplemente presenta valores de BSSRDF más bajos en general. Por otro lado, se observa también que, mientras que la BSSRDF de la muestra A es casi invariante con la geometría de medida, las muestras B y C sí presentan una variación entre las geometrías 1 y 2 y la geometría 3.
Además del IO-CSIC, el Conservatoire National des Arts et Métiers (CNAM), Instituto Designado en Francia para la radiometría, fotometría y espectrofotometría, ha diseñado también su propio sistema capaz de realizar medidas trazables de la BSSRDF, el cual comparte parte del gonio-espectrofotómetro desarrollado para medidas de la BRDF en superficies pequeñas [19]. Ambos institutos están llevando a cabo una comparación de sus respectivas escalas de medida de la BSSRDF para darles veracidad y poder transferirlas a otros laboratorios.
La definición de una escala de medida de la BSSRDF es un primer paso hacia la creación de una escala de medida de la translucidez, uno de los cuatro atributos perceptivos fundamentales de la apariencia visual [20]. No obstante, estudios recientes parecen indicar que la BSSRDF no es suficiente para caracterizar la reflectancia de materiales translúcidos, sino que una combinación de esta función junto con la BRDF sería necesaria para poder caracterizar por completo este tipo de materiales [21].
5. Conclusiones
El objetivo de este trabajo es crear la primera escala de medida de la BSSRDF y poder transferirla a otros centros de investigación o laboratorios para que puedan realizar medidas de esta función con trazabilidad al SI. Estas medidas son muy importantes para estudiar el scattering sub-superficial en materiales, también para entender mejor y poder reproducir la translucidez de estos. El sistema de medida desarrollado en el IO-CSIC ha sido evaluado y los resultados demuestran la capacidad del laboratorio para realizar esta escala. Se espera que, tras la caracterización completa del sistema y la identificación de todas las fuentes de incertidumbres correspondiente a esta medición, y una vez realizada la comparación con el sistema desarrollado en el CNAM, se pueda establecer la primera escala de medida de la BSSRDF y transferir el patrón a otros laboratorios para que puedan dar trazabilidad a sus medidas de esta función.
Bibliografía
- Nicodemus, F. E., et. al., “Geometrical considerations and nomenclature for reflectance.” NBS monograph 160:4 (1992).
- Venable, W. H., Describing spectrophotometric measurements, vol. 594 (US Department of Commerce, National Bureau of Standards, 1974).
- G. Obein, et. al., “New NIST reference goniospectrometer,” Proc. SPIE 5880, Optical Diagnostics, 58800T (2005).
- Hünerhoff, D., et. al., “New Robot-Based Gonioreflectometer for Measuring Spectral Diffuse Reflection.” Metrologia, 43 S11–S16 (2006).
- Baribeau, R., et. al., “Development of a Robot-Based Gonioreflectometer for Spectral BRDF Measurement.” J. Mod. Opt., 56 1497–1503 (2009).
- Rabal, A. M., et. al., “Automatic Goniospectrophotometer for the Absolute Measurement of the Spectral BRDF at In-and Out-of-Plane and Retroreflection Geometries.” Metrologia, 49 213–223 (2012).
- Basic, N., et. al., “Intercomparison of bidirectional reflectance distribution function (BRDF) measurements at in-and out-of-plane geometries.” (2023).
- Jensen, H. W., et. al., “A practical model for subsurface light transport,” Proc. ACM SIGGRAPH Conf. on Comput. Graph. pp. 511–518 (2001).
- Goesele, M., et. al., “DISCO – Acquisition of translucent objects,” ACM SIGGRAPH 2004 Pap. SIGGRAPH 2004 pp. 835–844 (2004).
- Lee, S. J., et. al., “Representation of homogeneous translucent materials using the P3 approximation and an image-based bidirectional subsurface scattering reflectance distribution function measurement system,” Opt. Eng. 49, 063601 (2010).
- Inoshita, C., et. al., “Full-dimensional sampling and analysis of BSSRDF,” IPSJ Transactions on Comput. Vis. Appl. 5, 119–123 (2013).
- Coppel, L. G., “Lateral light propagation and angular variation of the reflectance of paper,” Meas. Model. Reproducing Material Appear. 9018, 90180L (2014).
- Liang, S., et. al., “Rendering of 3d models based on bssrdf: A survey,” in 3D Imaging Technologies—Multi-dimensional Signal Processing and Deep Learning: Mathematical Approaches and Applications, Volume 1, (Springer, 2021), pp. 283–289.
- Frisvad, J. R., et. al., “Survey of Models for Acquiring the Optical Properties of Translucent Materials,” Comput. Graph. Forum 39, 729–755 (2020).
- Bernad, B., et. al., “Upgrade of goniospectrophtometer GEFE for near-field scattering and fluorescence radiance measurements,” in Meas. Model. Reproducing Material Appear. 9398, International Society for Optics and Photonics (SPIE), 105–115 (2015).
- Santafé-Gabarda, P., et. al., “Primary facility for traceable measurement of the BSSRDF.” Optics Express, 29(21), 34175-34188 (2021).
- Palmer, J. M. and Grant, B. G., The Art of Radiometry, Chapter 2 (SPIE, 2009).
- BIPM, Guide to the Expression of Uncertainty in Measurement. Paris, JCGM 100:2008 (2008).
- Saha, D., et. al., “Development of a μbrdf goniospectrophotometer for brdf measurement on tiny surfaces,” in Conference Proceeding by Commission Internationale de L’Eclairage (CIE), (2021).
- Ferrero, A., et. al., “Medida de la apariencia.” e-medida.es, 19 (2021).
- Ferrero, A., et. al., “Fundamental scattering quantities for the determination of reflectance and transmittance.” Optics Express 29(1), 219-231 (2021).
User Review
( votes)Summary









Comentarios