Ing. Luis Font Ávila
1. Introducción.
Con el aumento de las organizaciones que operan sistemas de gestión de la calidad u otros sistemas de gestión en los cuales se utilizan instrumentos de medida para asegurar el cumplimiento con los requisitos de un producto o proceso, es cada vez más frecuente la solicitud a los laboratorios de calibración por parte de sus clientes que se incluya en el certificado de calibración la conformidad del instrumento calibrado.
Mayormente el requerimiento proviene de clientes que necesitan demostrar que sus instrumentos son conformes para los procesos de medida donde son empleados. Aun cuando la necesidad está claramente especificada, es frecuente el hecho de que los clientes desconozcan lo que requiere el laboratorio de calibración para poder emitir dicho criterio y también el cómo definir los requisitos que debe cumplir el instrumento de medida para que este se encuentre conforme para el uso previsto.
Tradicionalmente, de forma errónea, el público interpreta a la calibración como el “ajuste del instrumento de medida”, por lo que muchos clientes de los laboratorios dan por hecho que un instrumento calibrado se encuentra “apto” para emitir resultados confiables.
El propósito de esta publicación es abordar el tema de la emisión de la conformidad de un instrumento o proceso de medida, desde el establecimiento de los requisitos de medición del cliente hasta la emisión de su conformidad, estando más enfocado hacia los clientes de los laboratorios que a los propios laboratorios.
Para profundizar en el tema que abordamos se recomienda a los lectores consultar los siguientes documentos:
- ISO 10012:2003 (es) “Sistemas de Gestión de las Mediciones — Requisitos para los Procesos de Medición y los Instrumentos de Medición”.
- JCGM 106:2012 “Evaluación de datos de medición – El papel de la incertidumbre de medida en la evaluación de la conformidad”.
- ILAC-G8:09/2019 “Guidelines on Decision Rules and Statements of Conformity”.
2. Requisitos de medición.
Según la norma ISO 10012, la organización debe asegurarse que el instrumento de medida es conforme con los requisitos correspondientes a su uso previsto, esta acción según la mencionada norma es llamada “confirmación metrológica” del instrumento de medida.
En base a lo anterior se deben establecer:
- Los requisitos metrológicos del proceso de medida: Se derivan de los requisitos para el producto y pueden considerar requisitos del cliente, de la organización, requisitos legales y reglamentarios en el caso de los procesos de medida sujetos al cumplimiento de reglamentaciones de metrología legal.
- Los requisitos metrológicos de los instrumentos de medida: Requisitos que el instrumento de medida debe cumplir para dar respuesta a los requisitos definidos en el inciso a).
Los requisitos pueden estar expresados como un error máximo permitido, incertidumbre objetivo, límites de medición, estabilidad, resolución, condiciones ambientales o habilidades del operador.
Un ejemplo de una reglamentación de metrología legal que define requisitos para los instrumentos de medida es la recomendación internacional de la OIML R 87: 2016 “Cantidad de producto en preempacados”. Dicha recomendación establece en el apartado 4.1.3 para aquellas organizaciones que manejan productos preenvasados lo siguiente… Las incertidumbres expandidas (al nivel de confianza k = 2) asociadas con los instrumentos de medición y los métodos de ensayo usados para determinar las cantidades no deben exceder 0,2 T…
Cuando se cuantifica la incertidumbre de medida asociada a la cantidad contenida de producto en el envase, se toma en cuenta el aporte de todos los instrumentos de medida y el propio método de ensayo y esta no debe ser mayor al requisito.
En la expresión anterior “T” es la deficiencia tolerable en la cantidad de un producto preempacado definida por la norma. Esto implica por ejemplo que, si la deficiencia tolerable para un producto con una masa nominal de 100 g es 4,5 g, entonces la incertidumbre expandida del proceso de determinación de la masa del producto no debe ser mayor que 0,9 g.
La incertidumbre expandida U(y) se obtiene multiplicando la incertidumbre típica combinada, uc(y), por un factor de cobertura k, en el ejemplo igual a 2.
3. Error máximo permitido del instrumento de medida.
De acuerdo con el Vocabulario Internacional de Metrología Conceptos fundamentales y generales, y términos asociados (VIM) el error máximo permitido de un instrumento de medición es el valor extremo del error de medida, con respecto a un valor de referencia conocido, permitido por especificaciones o reglamentaciones, para una medición, instrumento o sistema de medida dado, VIM [4.26].
El error máximo permitido para un instrumento de medida puede ser definido por una norma, una reglamentación metrológica, la documentación del fabricante o establecido por el propio usuario. A continuación, se enuncian algunos ejemplos:
- Error máximo permitido por una norma.
Para un termómetro de líquido en vidrio, modelo 9C la norma ASTM E1 (2020) “Standard specification for ASTM liquid-in-glass thermometers” establece un error en todo el intervalo de medida igual a 0,5 °C.
- Error máximo permitido por una reglamentación metrológica.
Para un instrumento de pesar de funcionamiento no automático los errores de medida determinados en su verificación periódica no deben superar el doble de lo establecido en la tabla 6 de la recomendación internacional de la OIML R 76-1: 2006 (E) “Non-automatic weighing instruments. Part 1: Metrological and technical requirements – Tests”.
- Error máximo permitido por un fabricante.
Para un multímetro digital en la medición de corriente eléctrica continua, el fabricante establece que el error es igual a (0,15 % de la lectura del multímetro + 1 dígito), donde el dígito es la resolución del instrumento.
- Error máximo permitido por el usuario.
Un método de ensayo requiere que se agreguen 100 g ± 1 g de un reactivo a una muestra. El usuario establece como error máximo permitido para la balanza utilizada en el pesaje un error máximo en 100 g igual a 0,1 g, considerando que el instrumento sea diez veces mejor que lo que establece el requisito de medida.
La calibración periódica de los instrumentos de medida nos permite conocer si los errores que realmente posee el instrumento se encuentran dentro del valor del error máximo permitido. Además de su calibración periódica, la organización debe contar con medios alternativos para asegurar el control del estado de calibración del instrumento entre calibraciones sucesivas.
4. Selección del instrumento de medida.
Cuando seleccionamos un instrumento de medida para un proceso en particular, debemos evaluar el requisito de metrológico del proceso, expresado como incertidumbre de medida esperada o tolerancia del producto, y el error máximo permitido del instrumento. Idealmente la relación entre el requisito metrológico del proceso y el error máximo permitido del instrumento debería ser tal que cualquier error de medida presente en el instrumento no afecte las decisiones que se tomen por la organización. Si el instrumento fue bien seleccionado, el error máximo permitido del mismo debe ser menor a los valores tolerados del proceso de medida en el cual será utilizado.
Por ejemplo, se desea medir la temperatura de pasteurización de un líquido, la cual por su naturaleza debe estar entre 62,80 °C y 65,56 °C, si consideramos un valor promedio dentro del intervalo anterior, la temperatura idealmente debe ser igual a 64,18 °C ± 1,38 °C, entonces un instrumento de medida con un error máximo permitido de 0,2 °C es adecuado para esta medición. La relación entre la tolerancia del proceso y el error máximo permitido del instrumento de medida es aproximadamente igual a 7. Más adelante en este artículo se aborda el concepto de índice de capacidad de medición.
Generalmente, un alto valor de esta relación resulta en un mayor costo de la medición, entre los factores que inciden se encuentran:
- La adquisición inicial del instrumento,
- Mantenimiento periódico,
- Ajuste,
- Actualizaciones del software o reparación,
- Calibración periódica,
- Entrenamiento del personal.
Lo anterior no debe ser pasado por alto, por lo que, debe buscarse un equilibrio entre el riesgo de una medición incorrecta sobre el producto y los costos del instrumento seleccionado.
De lo discutido anteriormente, queda claro que las organizaciones deben inicialmente definir los requisitos para sus procesos de medida y luego establecer qué requisitos metrológicos, deben cumplir los instrumentos de medida empleados en estos procesos.
Se debe evitar establecer requisitos metrológicos para los instrumentos de medida que resulten inadecuados, es decir, que no afecten el proceso de medición en el que estos instrumentos son utilizados, o que establezcan características que los instrumentos en cuestión no sean capaces de cumplir. Los requisitos para el instrumento se derivan de los requisitos del proceso donde son utilizados y no al contrario.
Una práctica errada, es considerar la resolución de los instrumentos indicadores, como una referencia de la exactitud de este o del proceso donde es utilizado, si bien es cierto que, para algunos tipos de instrumentos, el error máximo permitido es igual al valor de la resolución, esto no es aplicable para todos.
5. Incertidumbre del resultado de la medición.
La estimación del valor verdadero de una magnitud física se realiza por medio de una medición, considerando que su resultado es el mejor estimador de esta. Se debe tener en cuenta, que aun cuando este resultado es el mejor estimador, siempre tenemos un grado de duda, en que también el resultado representa al valor verdadero de la magnitud medida.
Esta duda se conoce como incertidumbre de medida y está definida en el vocabulario de metrología como el parámetro no negativo que caracteriza la dispersión de los valores atribuidos a un mensurando, a partir de la información que se utiliza (en la medición).
Al analizar los procesos de medición en una organización, nos encontraremos con la necesidad de conocer el valor de la incertidumbre de medida de nuestros procesos. Para dar respuesta a este problema, la organización debe contar con una metodología basada en el documento JCGM 100: 2008 “Evaluación de datos de medición – Guía para la expresión de la incertidumbre de medida” (GUM) y con personal formado para aplicarla.
Según la GUM, el resultado de una medición es sólo una aproximación o estimación del valor del mensurando, y únicamente se halla completo cuando está acompañado de una declaración acerca de la incertidumbre de dicha estimación.
Durante las auditorías a los procesos de medida, en ocasiones las organizaciones presentan como valor estimado de la incertidumbre de medida de sus procesos el valor que se indica para este parámetro en los certificados de calibración de sus equipos.
Para la estimación del valor de la incertidumbre asociada a un resultado, se debe utilizar la metodología descrita en la GUM.
- Establecimiento del modelo matemático de la medición.
Expresar matemáticamente la relación existente entre el mensurando Y y las magnitudes de entrada Xi de las cuales depende Y según la función Y=f(X1, X2…XN).
Nota: En los documentos que abordan el tema de la incertidumbre, la magnitud se representa con letra mayúscula y su estimación con letra minúscula.
- Determinar xi, el valor estimado de la magnitud de entrada Xi.
- Evaluar la incertidumbre típica u(xi) de cada estimación de entrada xi.
Emplear los métodos de evaluación de la incertidumbre típica Tipo A y Tipo B (no existe diferencia entre la naturaleza de la incertidumbre típica evaluada por ambos métodos).
- Evaluar las covarianzas asociadas a todas las estimaciones de entrada que estén correlacionadas u(xi; xj). Sí en el modelo matemático aparecen más de una magnitud de entrada se deben analizar la covarianza entre ellas.
En la mayoría de las mediciones para efectos prácticos se pueden considerar dos extremos; las magnitudes de entrada Xi, Xj no están correlacionadas o su correlación es máxima.
- Calcular el resultado de medición; esto es, la estimación y del mensurando Y, a partir de la relación funcional f utilizando para las magnitudes de entrada Xi las estimaciones xi.
- Considerando el modelo matemático de la medición y la ley de propagación de la incertidumbre, determinar la incertidumbre típica combinada uc(y) del resultado de medida y, a partir de las incertidumbres típicas u(xi) y covarianzas asociadas a las estimaciones de entrada.
- Si es necesario calcular una incertidumbre expandida U, cuyo fin es proporcionar un intervalo [y − U, y + U] en el que pueda esperarse encontrar la mayor parte de la distribución de valores que podrían, razonablemente, ser atribuidos al mensurando Y, multiplicando la incertidumbre típica combinada uc(y) por un factor de cobertura k.
Nota: El valor del factor de cobertura k se elige en función del nivel de confianza requerido para el intervalo de y − U a y + U. De acuerdo con la práctica internacional, se recomienda utilizar un factor de cobertura k = 2 en el cálculo de la incertidumbre expandida. Este valor de k dará una probabilidad de cobertura de aproximadamente 95,45 %, suponiendo una función de distribución normal (gaussiana), en la tabla 1 se suministran diferentes valores de k y sus niveles de confianza (asumiendo que la incertidumbre típica combinada uc(y) tiende a una función de distribución normal).
| Factor de cobertura k | Nivel de confianza % |
|---|---|
| 1,64 | 90 |
| 1,96 | 95 |
| 2,00 | 95,45 |
| 2,58 | 99 |
| 3,00 | 99,73 |
La incertidumbre de la calibración que informan los laboratorios en los certificados de calibración de los instrumentos es la duda que tienen esos laboratorios en el valor de la característica metrológica evaluada. Aun cuando el valor de esta característica, estimada en la calibración, es una magnitud de entrada xi con su correspondiente incertidumbre típica u(xi) asociada, no es la única magnitud de entrada que debe ser considerada en la incertidumbre de los procesos de medida donde el instrumento es empleado.
- Índice de capacidad de medición.
Según el documento JCGM 106:2012 el índice de capacidad de medición Cm es un parámetro que caracteriza la calidad de la medición, respecto a un requisito especificado por una tolerancia.
Se define como:
\(C_m=\frac{T}{2U}\)
(1)
Donde: T es la tolerancia del requisito especificado y U es la incertidumbre expandida asociada al resultado de medida.
Nota: La tolerancia es la diferencia entre los límites de tolerancia superior e inferior.
Por ejemplo, de acuerdo con la recomendación internacional de la OIML R 111-1: 2004 (E) “Weights of classes E1, E2, F1, F2, M1, M1–2, M2, M2–3 and M3. Part 1: Metrological and technical requirements”, una pesa con valor nominal de 200 g, clase de exactitud F1 tiene un error máximo permisible igual a 1 mg, por lo que la tolerancia es igual a 2 mg.
En la propia norma se establece el requisito para la incertidumbre de la calibración de las pesas indicando que esta debe ser menor o igual a 1/3 del error máximo permitido correspondiente a la clase de exactitud. Para la pesa anterior, la incertidumbre máxima de calibración que se podría informar es igual a 0,33 mg. El índice de capacidad para el proceso de calibración de la pesa es igual a:
\(C_m=\frac{T}{2U}=\frac{2\ mg}{2\times0,33\ mg}=3,03\approx3\)
Según al apartado 7.6.4 del JCGM 106: 2012 existe una estrecha conexión entre la capacidad de medición y otros parámetros derivados que se han utilizado para caracterizar la calidad de la medición en varios contextos. Entre ellos, está la relación tolerancia/incertidumbre de la calibración (TUR, del inglés Test Uncertainty Ratio) y la relación tolerancia/exactitud del ensayo (TAR, del inglés Test Accuracy Ratio).
\(TUR=\frac{T}{2U}=\frac{2\ \times E\ M\ P}{2\times U}=\frac{EMP}{U}\)
(2)
Donde: EMP es el error máximo permisible del instrumento bajo calibración y U(y) es la incertidumbre expandida de la calibración.
Dado que, normalmente la incertidumbre expandida se expresa para una probabilidad de cobertura de aproximadamente el 95 %, es una práctica generalmente aceptada que las declaraciones relativas al cumplimiento se relacionarán con el mismo nivel de confianza.
7. Declaración de conformidad de un instrumento de medida con una especificación metrológica.
En la evaluación de la conformidad de un instrumento de medida realizada a partir del resultado de su calibración, se utiliza el resultado de la característica metrológica evaluada y los límites de la especificación metrológica.
Si el “valor verdadero de la propiedad” se encuentra dentro del intervalo de tolerancia, se dice que hay conformidad, y de no ser así, se dice que no hay conformidad.
La emisión de la conformidad debe no sólo considerar al propio resultado y los límites de la especificación, debe tener en cuenta también la incertidumbre asociada a ese resultado.
Si la relación entre la incertidumbre del resultado de la medición es igual a 10 o mayor, entonces se puede aplicar utilizar una regla de decisión basada en la aceptación simple, en caso contrario se debe evaluar la necesidad de utilizar una regla de decisión basada en zonas de seguridad.
8. Decisión basada en la aceptación simple según JCGM 106: 2012.
La regla de decisión, para emitir conformidad con una especificación, es la definición de cómo se utiliza la incertidumbre de medida junto al resultado para emitir este dictamen.
En la práctica el valor del TUR puede ser utilizado para decidir cual regla de decisión aplicar.
Si el valor del TUR es mayor o igual que 10, se puede emplear una regla de decisión simple, también conocida como regla de aceptación basada en el “riesgo compartido” por el laboratorio de calibración y el cliente (propietario del equipo de medida).
Según esta regla de decisión todo resultado de medida, sin considerar la incertidumbre asociada al mismo, que se encuentre dentro de los limites de la especificación es conforme y todo aquel que se encuentre fuera esta no conforme.
Es importante reconocer el hecho de que todo resultado tiene una incertidumbre asociada a él, la cuestión está en definir si la misma es apropiada para el fin previsto. Por ejemplo, se calibra un termómetro de líquido en vidrio que posee un EMP igual a, 1 °C con una incertidumbre expandida de calibración igual a 0,010 °C asegurando una relación de 10 (TUR) es decir la calidad de la calibración, evaluada a través de su incertidumbre, es aproximadamente 10 veces mejor que la tolerancia del instrumento bajo calibración.
Cuando el TUR no es tan elevado, se debería implementar la decisión considerando zonas de seguridad para reducir el riesgo de una decisión errónea en base a los resultados.
9. Reglas de decisión basadas en zonas de seguridad.
La regla de decisión basada en zonas de seguridad considera el cálculo de una zona de seguridad a partir de los límites de la especificación y la incertidumbre del resultado de la medición.

Los límites de la zona de seguridad se denominan límites de aceptación [LA], los cuales se estiman a partir de los límites de la especificación [LA] menos el valor W denominado zona de seguridad.
\(LA=LS-W\)
(3)
Donde W es la zona de seguridad.
De acuerdo con el ejemplo 3 del documento publicado por la ILAC G8, el valor del límite de aceptación se puede estimar como:
\(LA=\sqrt{{LS}^2-U^2}\)
(4)
Según lo publicado por el documento ILAC G8 en la tabla 1 el límite de aceptación estimado por la ecuación 4 asegura un nivel de riesgo menor al 2,5 % de decisión errónea en base a los resultados.
A continuación, en la figura 3 se muestra un ejemplo del uso de la regla de decisión basada en zonas de seguridad considerando el gráfico de 2 del ILAC G8.
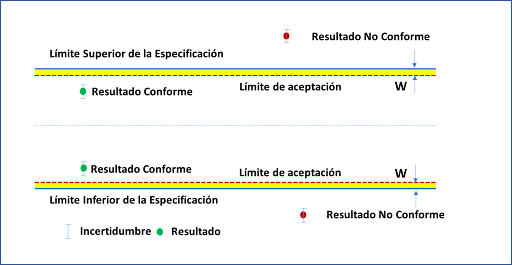
La regla de decisión debe ser establecida por la organización considerando el riesgo de aceptar como conforme un equipo de medición. En algunos casos las organizaciones implementan la regla de decisión que se muestra en la figura 4, en la cual cualquier resultado expandido en la incertidumbre que presente posibles valores en la zona de seguridad se considera como no conforme.
10. Conclusiones.
Las organizaciones que requieren evaluar que sus instrumentos de medida se encuentran conformes para los procesos donde son empleados deben establecer en una primera fase los requisitos metrológicos para dichos procesos y luego los requisitos metrológicos para los instrumentos de medida, esta acción es responsabilidad exclusiva de la propia organización.
Para poder emitir la conformidad de un proceso de medida (o instrumento de medida) con dicha especificación es necesario definir cuál regla de decisión aplicar, considerando el índice de capacidad del proceso.
Si el proceso de medida tiene un índice de capacidad igual o mayor a 10 pueden manejarse con una regla de decisión simple, para el resto de los casos se debe evaluar como el riesgo de una decisión errada afecta al producto o al proceso de medida y se debe evaluar la conveniencia de emplear una regla de decisión que utilice zonas de seguridad.
11. Bibliografía.
[1] OIML R 87: 2016 Cantidad de producto en preempacados.
[2] ISO 10012: 2003 (es) Sistemas de gestión de las mediciones – Requisitos para los procesos de medición y los instrumentos de medición.
[3] JCGM 100: 2008 Evaluación de datos de medición – Guía para la expresión de la incertidumbre de medida (GUM).
[4] JCGM 106: 2012 “Evaluación de datos de medición – El papel de la incertidumbre de medida en la evaluación de la conformidad”.
[5] ILAC-G8:09/2019 Guidelines on decision rules and statements of conformity.
[6] JCGM 200:2012 Vocabulario Internacional de Metrología Conceptos fundamentales y generales, y términos asociados (VIM).
[7] ASTM E1-14(2020) Standard specification for ASTM liquid-in-glass thermometers.
[8] OIML R 76-1: 2006 (E) Non-automatic weighing instruments. Part 1: Metrological and technical requirements – Tests.
[9] OIML R 111-1: 2004 (E) Weights of classes E1, E2, F1, F2, M1, M1–2, M2, M2–3 and M3. Part 1: Metrological and technical requirements.










Comentarios