Jose J. Segovia
Mª del Carmen Martín
Grupo de Investigación TermoCal
Instituto de Bioeconomía
Universidad de Valladolid
RESUMEN
La capacidad calorífica de un líquido es una propiedad termodinámica básica y su conocimiento es necesario para la ingeniería, en el diseño, la simulación y el control de procesos, que implican, entre otros, la realización de balances de energía. Además, es una fuente de información muy importante para discernir la estructura y las interacciones moleculares de las soluciones líquidas, que sirven de base para el desarrollo de los modelos utilizados en la industria.
La determinación experimental de capacidades caloríficas se realiza con calorímetros que permiten medir la energía entrante en el sistema y el incremento en la temperatura que provoca. Los calorímetros pueden ser estáticos o con flujo según la técnica de manipulación de las sustancias.
Los datos experimentales de esta propiedad son escasos, tanto por el número de sustancias estudiadas, como por las condiciones, normalmente a temperaturas próximas al ambiente y a presión atmosférica.
ABSTRACT
Liquid heat capacity is a key thermodynamic property and its knowledge is required in engineering for design, simulation and control of processes, where energy balances are involved. Moreover, it is a source of very important information for understanding the structure and molecular interactions in liquid solutions which are the base for the development of models used in industry.
Experimental measurement of heat capacities is carried out by means of calorimeters which measure the input of energy in the system and the corresponding increase in temperature. There are static or flow calorimeters depending on the way of handling the sample.
Scarce data of this property are available due both to number of studied compounds and measurement conditions, usually close to ambient temperature and atmospheric pressure.
Palabras clave: Capacidad calorífica, líquido, propiedad termodinámica.
1. INTRODUCCIÓN
En la actualidad, cualquier sociedad quisiera disponer de unas sanas infraestructuras de las que beneficiarse por medio de lo que hoy en día se entiende como sostenibilidad. Sostenibilidad significa “hacer frente a las necesidades del presente sin comprometer la capacidad de las futuras generaciones de resolver sus propias necesidades”. Tiene tres ejes interdependientes y mutuamente reforzadores: (i) el desarrollo económico, (ii) el desarrollo social, y (iii) la protección ambiental. Pueden incorporarse a la sociedad a través de lo que comúnmente se llama “Infraestructura de la Calidad” que incluye como tres pilares fundamentales de la sostenibilidad:
- la normativa técnica
- la evaluación de la conformidad
- la metrología
Su ejecución efectiva permitirá la sostenibilidad y la creación de bienestar en la sociedad. Una herramienta esencial para garantizar todos estos aspectos requeridos para un desarrollo sostenible de las naciones es su capacidad de poder determinar medidas precisas y fiables.
Operaciones de ingeniería como el diseño, la simulación y el control de procesos, que implican entre otros la realización de balances de energía, requieren de un conocimiento exacto de las propiedades termodinámicas y el comportamiento de las mezclas. Aun cuando se utilicen modelos que permitan evaluar propiedades termodinámicas sin ser medidas, los modelos deben contrastarse con datos experimentales [1]. La capacidad calorífica de líquido es una propiedad termodinámica básica y su conocimiento, no sólo es necesario para la ingeniería, sino que también es una fuente de información muy importante para discernir la estructura y las interacciones moleculares de las soluciones líquidas, que sirven de base para el desarrollo de los modelos utilizados en la industria. Los datos experimentales de esta propiedad son escasos, tanto por el número de sustancias estudiadas, como por las condiciones, normalmente a temperaturas próximas al ambiente y a presión atmosférica [2].
2. CAPACIDAD CALORÍFICA DE LÍQUIDOS
La capacidad calorífica representa la relación entre la energía térmica intercambiada por el sistema y el efecto en temperatura que provoca en un proceso, resulta clave definir el proceso o camino a través del cual evoluciona el sistema.
\(C_{\textrm{proceso}}=\left ( \frac{{\partial}’ Q}{\partial T} \right )_ \textrm{proceso} \)
(1)
A través de las relaciones termodinámicas permite obtener los cambios en energía interna, entalpía, energía libre de Gibbs y entropía. Los datos de capacidad calorífica en amplios intervalos de presión y temperatura, si se complementan con propiedades p,V,T, sirven a su vez para obtener otras propiedades termodinámicas y proporcionan un conocimiento termodinámico completo del sistema [3]. La primera derivada de la entalpía y la segunda de la energía libre de Gibbs es la capacidad calorífica a presión constante, Cp.
\(C_{p}=\left ( \frac{\partial H}{\partial T} \right )_{p,x} =-T\left ( \frac{\partial^{2} G}{\partial T^{2}} \right )_{p,x}=T\left ( \frac{\partial S}{\partial T} \right )_{p,x} \)
(2)
La primera derivada de la energía interna es la capacidad calorífica a volumen constante, CV.
\(C_{v}=\left ( \frac{\partial U}{\partial T} \right )_{v,x} \)
(3)
Para poder discutir las técnicas experimentales y sus aplicaciones, es necesario revisar las relaciones termodinámicas más relevantes para las capacidades caloríficas [4].
La dependencia de la capacidad calorífica con la presión o con el volumen se puede determinar a partir de datos p, V, T, mientras que la dependencia con la temperatura hay que determinarla calorimétricamente.
\(\left ( \frac{\partial C_{p}}{\partial p} \right)_{T}=-T\left ( \frac{\partial^{2} V}{\partial T^{2}} \right)_{p}\)
(4)
\(\left ( \frac{\partial C_{v}}{\partial V} \right)_{T}=-T\left ( \frac{\partial^{2} p}{\partial T^{2}} \right)_{v}\)
(5)
En general, es más usual realizar medidas de las capacidades caloríficas a presión constante, Cp, que, de la capacidad calorífica a volumen constante, CV, por lo que se necesita conocer las relaciones entre ambas, que vienen dadas como:
\(C_{p}-C_{v}= \frac{TV\alpha_{p}^{2}}{K_{T}} \)
(6)
\(\gamma = \frac{C_{p}}{C_{v}}=\frac{K_{T}}{K_{S}}\)
(7)
Donde αp es el coeficiente de expansión térmica isobárica, κT el coeficiente de compresibilidad isotermo, κS el coeficiente de compresibilidad isentrópico y \(\gamma\) el coeficiente adiabático.
\(\alpha_{p}= \frac{1}{V}\left(\frac{\partial V}{\partial T}\right)_{P}=\left(\frac{\partial l\ n{V}}{\partial T}\right)_{P}\)
(8)
\(K_{T}= -\frac{1}{V}\left(\frac{\partial V}{\partial p}\right)_{T}=\left(\frac{\partial l\ n{V}}{\partial p}\right)_{T}\)
(9)
\(K_{S}= -\frac{1}{V}\left(\frac{\partial V}{\partial p}\right)_{S}\)
(10)
Además de Cp y CV hay otras dos capacidades caloríficas de uso común para líquidos, Cσ y Csat, que representan, la primera, la variación de la entalpía con la temperatura de un líquido saturado y la segunda, la energía requerida para provocar un cambio en la temperatura de un líquido saturado manteniendo su estado. La relación de estas con Cp viene dada por:
\(C_{\sigma}=\frac{dH_{\sigma}}{dT}=C_{p}+\left [ V_{\sigma}-T\left ( \frac{\partial V}{\partial T} \right )_{p} \right ]\left (\frac{dP}{dT} \right )_{\sigma }=C_{\textrm{sat}}+V_{\sigma} \left ( \frac{dP}{dT} \right )_{\sigma } \)
(11)
3. DETERMINACIÓN EXPERIMENTAL
Un calorímetro para la determinación de capacidades caloríficas consiste en un recipiente adiabático con dispositivos de medida de la energía entrante y del incremento de la temperatura [5].
Admitiendo que el volumen del líquido no cambia con el incremento de la temperatura y que las pérdidas del sistema se pueden evaluar, al aplicar una energía Welect, que provoque un cambio de T1 a T2, el primer principio de la termodinámica conduce a:
\(U_{2}-U_{1}=Q_{\textrm{perd}}-\int_{v_{1}}^{v_{2}}pdV+W_{\textrm{elect}} \)
(12)
Donde la variación de la energía interna es igual al trabajo por cambio de volumen, junto al trabajo eléctrico, y las pérdidas de energía (tan pequeñas como sea posible).
Una determinación de la capacidad calorífica consiste en llenar el recipiente con una muestra líquida y aplicar la energía necesaria para provocar un cambio de T1 a T2. El experimento se repite sin muestra. Admitiendo que los estados inicial y final del recipiente en cada determinación son los mismos, que el volumen del líquido no cambia con el incremento de la temperatura, que las pérdidas del sistema son idénticas en cada caso, y que no hay reacción química, entonces:
\(U\left (T_{2′} V \right )-U\left ( T_{1′}V \right )=W_{\textrm{elect}}(\textrm{líquido+recipiente})-W_{\textrm{elect}}(\textrm{recipiente})=\int_{T_{1}}^{T_{2}}C_{v}dT \)
(13)
Donde
\(C_{V}=\left ( \frac{\partial U}{\partial T} \right )_{V}=\displaystyle \lim_{T_{2} \to T_{1}}\left ( \frac{ W_{\textrm{elect}}(\textrm{líquido+recipiente})-W_{\textrm{elect}}(\textrm{recipiente}) }{T_{2}-T{1}} \right ) \)
(14)
La dificultad de medir a volumen constante hace que muy pocos calorímetros estén diseñados para medir directamente CV.
La mayor parte de las técnicas calorimétricas operan a presión constante y, por tanto, miden la capacidad calorífica isobárica, Cp. Las medidas se pueden realizar por métodos estáticos, con la muestra confinada en un recipiente, o dinámicos, cuando la muestra circula por la celda de medida.
Los calorímetros de flujo eliminan la fase vapor y proporcionan resultados rápidos y de gran exactitud. La capacidad calorífica isobárica se obtiene determinando la energía eléctrica aplicada al fluido que pasa a través del calorímetro con un flujo constante y que provoca un cambio en la temperatura.
En un calorímetro de flujo, donde la presión permanece constante, la diferencia entre el flujo entálpico de salida menos el de entrada es igual al flujo de calor puesto en juego:
\(\dot{n}H_m\left(T_2,p\right)-\dot{n}H_m\left(T_1,p\right)=\dot{Q}\)
(15)
Donde:
\(C_{p,m}=\left(\frac{\partial H_m}{\partial T}\right)_p=\displaystyle \lim_{T_{2} \to T_{1}}\begin{Bmatrix}\frac{\dot{Q}}{\dot{n}\left ( T_{2}-T_{1} \right )} \end{Bmatrix} \)
(16)
Siendo n el flujo molar, H la entalpía y Q el flujo de calor.
La figura 1 muestra el esquema de un calorímetro adiabático de flujo.
En un calorímetro donde la fase vapor tiene espacio para acomodar la expansión de la muestra durante el calentamiento, la presión del sistema es la presión de vapor, estamos determinando la capacidad calorífica a lo largo de la curva de saturación donde la temperatura y la presión están claramente definidas. La capacidad calorífica determinada es entonces la capacidad calorífica del líquido saturado Csat. La relación capacidad calorífica del líquido en equilibrio con el vapor y la capacidad calorífica isobárica se ha mostrado en la ecuación 11.
Una breve clasificación de las técnicas para la medida de capacidades caloríficas se muestra en la figura 2.
Entre los métodos dinámicos, para la medida de la capacidad calorífica a presión constante, destacamos los calorímetros tipo Picker, los calorímetros de flujo de calor y los adiabáticos, y entre los estáticos, los calorímetros de flujo de calor, los de escaneo diferencial y los adiabáticos, [6]. A continuación, comentaremos más en detalle alguno de ellos.
Calorímetro de flujo tipo Picker.
El calorímetro diseñado por Patrick Picker [7] consta de dos células idénticas montadas en serie como se muestra en la figura 3. Cada célula tiene un calentador tipo Zener, Z1 y Z2, y dos termistores, T1 y T2, para la medida de la temperatura del fluido después de ser calentado. A la entrada, el líquido está termostatizado a la temperatura T0. El calorímetro utiliza un fluido de referencia de capacidad calorífica conocida, siendo \( \dot{W}_{0}\) la potencia de base disipada en los diodos para mantener una diferencia de temperatura entre la entrada y la salida, ΔT, normalmente de 1 K.
Cuando se introduce la muestra, la diferencia en la temperatura de equilibrio se debe a una diferencia en la capacidad calorífica entre el líquido patrón y la muestra. Un método de trabajo consiste en variar la potencia, ΔW, para conseguir, con el mismo flujo volumétrico, la misma temperatura de salida. La relación de base entre las capacidades caloríficas volumétricas del patrón de referencia y la muestra es la siguiente:
\(\left(\frac{C_{p,m}}{V_m}\right)_{\textrm{muestra}}/\left(\frac{C{p,m}}{V_m}\right)_{\textrm{patrón}}=1+\left ( \frac{\Delta \dot{W}}{\dot{W}_{0}} \right )\)
(17)
Esta técnica, diseñada por Picker, supuso un hito en la calorimetría, siendo capaz de determinar, con una gran exactitud, la capacidad calorífica de pequeñas muestras de líquidos. Estos calorímetros han sido la base de los modernos calorímetros de flujo.
Calorímetro de flujo de calor estático.
En un calorímetro de flujo de calor estático la muestra permanece confinada en un recipiente. Un gran número de termopares conectan los recipientes que contienen las muestras con el termostato y constituyen la termopila, permitiendo la disipación de energía, como se muestra en la figura 4. Cuando las dos termopilas, conectadas a sus respectivas celdas, operan a la misma temperatura, por estar en el mismo termostato, es posible determinar el flujo de calor entre las dos termopilas. Este efecto es conocido como principio Calvet [8]. La figura 4 muestra un esquema del calorímetro.
Las principales ventajas del calorímetro son el pequeño tamaño de muestra y el control de la temperatura de las termopilas con el termostato.
El calorímetro requiere calibración en vacío y con un fluido de calibración, normalmente agua.
En una medida se colocan la muestra y un líquido de referencia en las celdas. La referencia se escoge de modo que tenga una capacidad calorífica volumétrica conocida y cercana a la muestra. El calorímetro se programa en pasos con un ΔT (normalmente 1 K), registrando el flujo de calor mientras se incrementa la temperatura. La capacidad calorífica volumétrica se puede evaluar como:
\(\left(\frac{C_{p,m}}{V_m}\right)_X=\left(\frac{C_{p,m}}{V_m}\right)_R+\left(\frac{C_{p,m}}{V_m}\right)_W\frac{\left\{S\left(X,R\right)-S(R,R)\right\}}{\left\{S(W,E)-S(E,E)\right\}}\)
(18)
Donde X es la muestra, R la referencia, W el agua y E indica vacío.
La determinación de las rampas de temperatura y los flujos de calor hacen que las incertidumbres sean altas, 2,5 %, [9].
Calorímetro de flujo con flujo de calor.
La técnica está basada en la utilización conjunta de una potencia refrigeradora y una calefactora que actúan sobre la celda de flujo del calorímetro, figura 5. Bajo este principio, la casa norteamericana Hart-Scientific comercializó un calorímetro de flujo isotermo para la medida de entalpías de mezcla.
El calorímetro permite relacionar una cantidad de energía conocida aplicada al flujo, con el incremento en la temperatura del fluido, evaluando también todas las interacciones energéticas del sistema con su entorno, [10].
El fluido es impulsado por una bomba y circula por un tubo de acero inoxidable arrollado y soldado sobre un bloque de cobre. El bloque permite que se trasmita por conducción toda la energía térmica implicada en el proceso. El líquido entra en la célula de flujo a una temperatura T1. Un dispositivo Peltier y una resistencia eléctrica, situados en la zona de salida se encargan de provocar que el líquido salga a la temperatura deseada T2, fijando así el salto térmico del fluido a su paso por la celda de medida. El calorímetro trabaja con un incremento de temperatura constante, normalmente 0,5 K.
El Peltier se alimenta con una fuente de corriente continua y provoca un flujo de calor fijo desde la celda al baño. Para compensar esta pérdida y mantener la temperatura de salida de la celda constante, un generador de pulsos de frecuencia constante, y tiempo de pulso variable, alimenta la resistencia de control compensando todas las contribuciones energéticas, y estableciendo el salto de temperatura deseado.
El valor de la potencia neta suministrada en la resistencia de control se relaciona directamente con la capacidad calorífica a presión constante.
\(C_p=\frac{{\dot{Q}}_{net}}{\dot{m}\cdot\Delta T}=\frac{{\dot{Q}}_{net}}{\dot{V}\cdot\rho\cdot\Delta T}\)
(19)
Donde \({\dot{Q}}_{net}\) es la potencia eléctrica neta disipada en la resistencia de control, m el flujo másico, \( \dot{V} \) el flujo volumétrico, ρ la densidad y ΔT el salto de temperatura, normalmente 0,5 K.
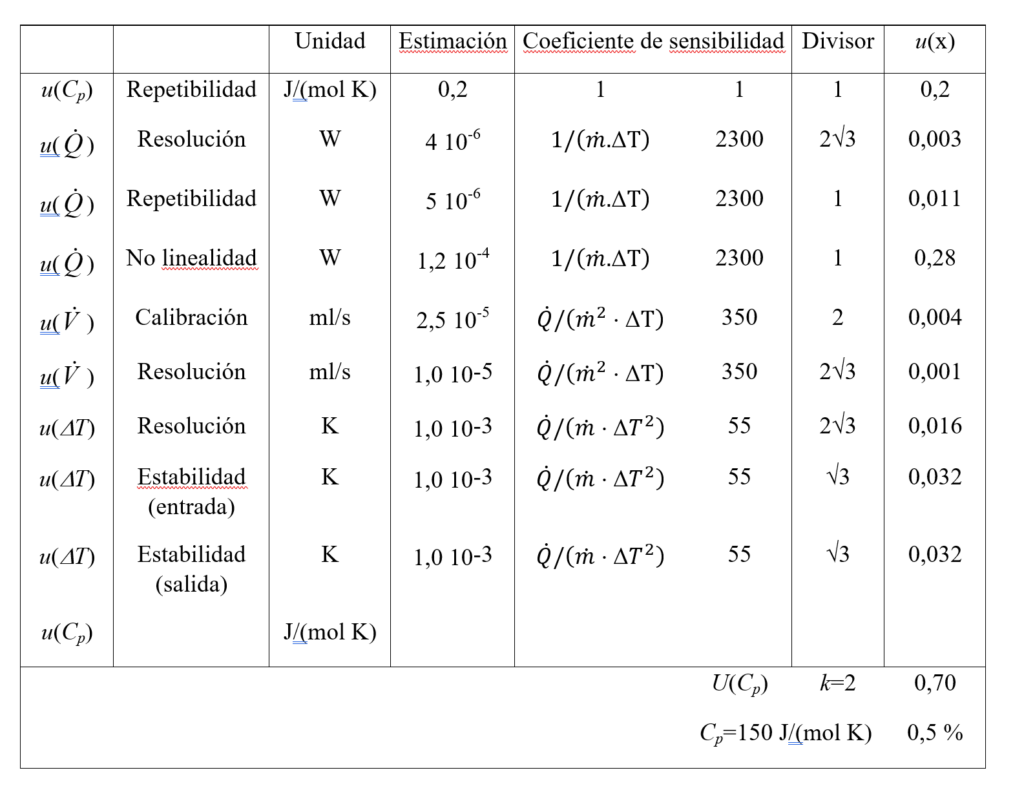
La calibración eléctrica del equipo se realiza con la simulación de diferentes energías mediante efecto Joule. Durante el calibrado, las condiciones de refrigeración y de temperatura a la salida se mantienen como en la medida real. Las incertidumbres de medida de la magnitud de salida, Cp, en función de las magnitudes medidas, se muestran en la tabla 1. Las incertidumbres expandidas (k=2) de la medida de la temperatura y la presión a las cuales se determina Cp=f(T,p) son; U(T)= 10 mK y U(p)=0,02 % de la presión medida respectivamente.
4. CONCLUSIONES
La capacidad calorífica de líquido es una propiedad termofísica esencial y proporciona información sobre la estructura y las interacciones moleculares de las soluciones líquidas. Es fundamental en la ingeniería para los procesos que implican la realización de balances de energía.
Podemos clasificar las diferentes técnicas experimentales atendiendo a la manipulación de las sustancias y al flujo de energía. En este trabajo se han presentado tres técnicas, las dos primeras han supuesto un hito en la calorimetría y son la base de los calorímetros actuales. El calorímetro tipo Picker para las técnicas de flujo y el calorímetro tipo Calvet para las técnicas estáticas.
La tercera técnica presenta un calorímetro de flujo con flujo de calor, que presenta una baja incertidumbre, en el límite de la técnica, para la medida de esta propiedad.
BIBLIOGRAFÍA
[1] Prausnitz J., Lichtenthaler R.N.; Azevedo E.G., 2000. “Termodinámica molecular de los equilibrios de fases”, 3ra Edición, Prentice-Hall, PTR.
[2] Zábranský M., Růžička V., 2002. “Heat capacity of liquids: a survey and data needs”, Fluid Phase Equilibria, 194 (1), 817-824.
[3] Smith J.M., Van Ness H.C., Abbott M.M.,1997. “Introducción a la Termodinámica en Ingeniería Química”, 5ª Ed., McGraw-Hill, México.
[4] Grolier J.P.E., 1997. “Fluid-phase calorimetry and more: A longtime relationship with chemical thermodynamics”, Thermochimica Acta 300, 149-157.
[5] Marsh K.N., O’Hare P.A.G. (Editors) 1994. “Solution Calorimetry. Experimental Thermodynamics. Volume IV”. IUPAC Commission on Thermodynamics. Blackwell Scientific Publications, Oxford.
[6] Goodwin A.R.H., Marsh, K.N., Wakeham, W.A. (Editors) 2003. “Measurement of the Thermodynamics Properties of Single Phases. Volume VI”. IUPAC Commission on Thermodynamics, Elsevier, Amsterdan.
[7] Picker P., Leduc P-A, Phipip P.R. and Desnoyers J.E., 1971. “Heat capacity of solutions by flow microcalorimetry”. Journal of Chemical Thermodynamics 3, 631-642.
[8] Calvet E. and Prat H. “Microcalorimétrie. Applications Physico-Chimiques et Biologiques”. Maison, Paris, 1956.
[9] Rudtsch S., 2002. “Uncertainty of heat capacity measurements with differential scanning calorimeters”, Thermochim. Acta 382, 17-25.
[10] Segovia J.J., Vega-Maza D., Chamorro C.R., Martín M.C., 2008. “High-pressure isobaric heat capacities using a new flow calorimeter”, Journal of Supercritical Fluids 46, 258-264.










Comentarios