José Juan Segovia, David Vega
Universidad de Valladolid, Grupo de Investigación TERMOCAL. Escuela de Ingenierías Industriales, Paseo del Cauce 59, Valladolid
Teléfono: +34 983184690; e-mail: jose.segovia@eii.uva.es
RESUMEN
La densidad es una propiedad termofísica fundamental que debe ser caracterizada con exactitud en un rango amplio de temperaturas, presiones y composiciones. Las ecuaciones de estado que la caracterizan deben ser validados por medidas experimentales de muy baja incertidumbre. Presentamos aquí ecuaciones de estado fundamentales para modelar la densidad de gases ideales y reales, y aquellas que estudian el comportamiento de gases y líquidos.
Experimentalmente, la densidad de líquidos a presiones ambiente puede ser determinado con un picnómetro. En un rango elevado de presiones y temperaturas puede ser medida con densímetros de tubo vibrante calibrados con líquidos de referencia, densímetros profusamente utilizados en la industria y la investigación. Las densidades de los gases son caracterizadas con balanzas hidrostáticas. Las de suspensión magnética alcanzan las menores incertidumbres.
ABSTRACT
Density is a fundamental thermophysical property. It should be characterised in a wide range of pressures, temperatures, and compositions. Low uncertainty experimental density measurements validate equations of state that characterise density. This paper present fundamental equations of state modelling ideal and real gas densities. Gas and liquid behaviour are also modelled by appropriate equations of state.
Ambient pressure liquid densities can be experimentally gathered using pycnometers. Vibrating tube densimeters measure density in a wide range of pressures and temperatures. The latter require a calibration with two reference fluids. They are widely used by the industry and the research community. Gas densities are measured with hydrostatic balances. Magnetic suspension balance densimeters present the lowest uncertainties.
Palabras clave: densidad, gas, líquido, ecuación de estado.
1. INTRODUCCIÓN
La densidad es una propiedad termofísica fundamental de toda sustancia. Se define como la razón de la masa por unidad de volumen que ocupa y su símbolo es ρ. Las unidades en el sistema internacional son kg·m-3.
El inverso de la densidad se define como el volumen específico, υ:
\(\rho=\frac{masa}{volumen}=\frac{1}{\upsilon}\ .\)
Para una sustancia simple compresible, dos propiedades intrínsecas independientes fijan el estado intensivo, existiendo una ecuación que relaciona estas dos propiedades con una tercera propiedad dependiente. Las propiedades intrínsecas de interés para un sistema fluido son la presión, la temperatura y el volumen, P, T y υ. La relación entre éstas la define la ecuación de estado.
Las propiedades termofísicas son fundamentales para el conocimiento y solución de los grandes problemas del mundo: crisis energética, calentamiento global, deterioro del medio ambiente, agotamiento de los recursos naturales, etc. En particular, la densidad es necesaria en el diseño de procesos industriales, dimensionamiento de instalaciones, transferencia de fluidos, conversión de flujos volumétricos en másicos y un largo etcétera.
La principal fuerza conductora para el uso de propiedades termofísicas en la industria ha sido la reducción de costos, tanto de instalación como de funcionamiento. Se han identificado más de 15000 sustancias puras de interés para la industria, pero solo hay datos experimentales, de buena calidad, para unos pocos compuestos y en condiciones próximas a presión y temperatura ambiente (Gupta and Olson, 2003). A esta deficiencia en datos para sustancias puras hay que añadir el estudio de las mezclas, lo que hace inabordable el problema únicamente desde la experimentación. De aquí la necesidad de apoyarnos en métodos de estimación teóricos, empíricos o semiempíricos, que deben ser validados con datos experimentales de alta exactitud. Como ejemplo, la industria del gas natural en USA realizó una estimación conservadora en donde, por cada dólar invertido en investigación en propiedades termofísicas, se puede atribuir un ahorro de costes directos de 12 dólares (Elliot et al., 1996).
2. ECUACIÓN DE ESTADO
La ecuación de estado de una sustancia pura se expresa a partir de la relación de sus variables PυT, o PρT, y se puede representar como una superficie en un espacio tridimensional. Las coordenadas son las propiedades y muestra la estructura básica de la materia. Los diagramas representan los estados de equilibrio y son muy útiles para introducir las relaciones generales de los estados de la materia. La figura 1 muestra la superficie PυT de una sustancia pura que se expansiona al solidificar, como el agua.
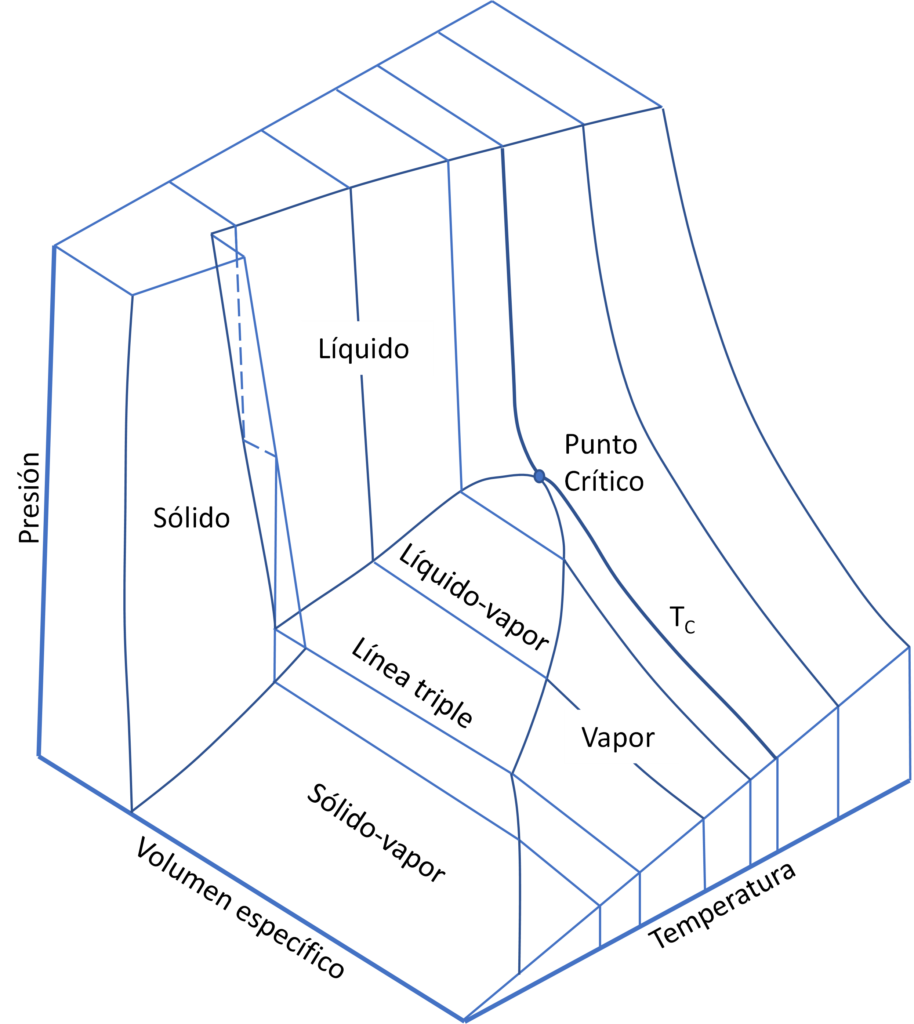
Una ecuación de estado nos proporciona una relación matemática entre la presión, la temperatura, y el volumen. Esta relación se puede expresar en forma de ecuación, gráficos, o tablas de valores numéricos. Las medidas de la ecuación de estado PυT, comienzan en los siglos XVII y XVIII con los trabajos de Boyle y Charles, con lo que hoy conocemos como ley de los gases ideales. J. Canton fue el primero que mostró que los líquidos son compresibles y perfectamente elásticos en 1762. La ley de los gases ideales se expresa como
\(Pv=RT\ ,\)
Donde R es la constante universal de los gases. υ se refiere al volumen específico molar.
Los gases reales presentan desviaciones de esta ecuación. Solo se aproximan a este comportamiento a baja presión. Se han propuesto muchas modificaciones de esta expresión, empíricas o semiempíricas, como la ecuación de virial, que consiste en una serie de potencias de la densidad. Esta ecuación solo describe el comportamiento de gases:
\(P\upsilon=RT\left(\frac{B}{\upsilon}+\frac{C}{\upsilon^2}\ldots.\right),\)
donde B, C, … son el segundo, tercer y siguientes coeficientes de virial.
Las ecuaciones analíticas de estado describen el comportamiento de gases y líquidos y tienen que ser, como mínimo, cubicas en el volumen. Todas ellas expresan P como una función de υ, T a través de unos parámetros que dependen de la naturaleza de cada sustancia. Estas ecuaciones parten de la ecuación seminal de van der Waals (1890)
\(P=\frac{RT}{\upsilon-b}-\frac{a}{\upsilon^2}\ ,\)
en donde a y b son parámetros específicos de cada sustancia.
Si trabajamos con mezclas, los parámetros se pueden obtener por ponderación de los parámetros de los compuestos puros que forman la mezcla a través de las llamadas reglas de mezcla.
Resulta evidente que la aplicabilidad de estas ecuaciones depende tanto de su capacidad para representar la superficie de estado como de la exactitud en la determinación de los coeficientes a través de la experimentación.
Allí donde no existan valores experimentales de la densidad a la presión y temperaturas deseadas, estas expresiones matemáticas de la ecuación de estado nos permiten estimar o predecir el valor de aquella.
3. DETERMINACIÓN EXPERIMENTAL DE LA DENSIDAD
La determinación experimental de la densidad de líquidos y gases ha sido extensamente tratada en los trabajos de la IUPAC (Neindre et al. 1975) y (Goodwin et al. 2002). En este trabajo destacaremos algunos de los métodos que, por su sencillez o su exactitud, son los más empleados en la actualidad.
3.1. Picnometría de líquidos.
Un picnómetro consiste en un recipiente que contiene la muestra, de volumen conocido, y donde podremos conocer la masa, a través de la diferencia entre el recipiente lleno y vacío. La densidad será entonces el cociente entra la masa y el volumen. Los equipos más sencillos nos proporcionan valores de densidad de líquidos en condiciones próximas al ambiente con incertidumbres relativas inferiores a ± 0,1 %.

La calibración del volumen se puede realizar con agua a cada temperatura de uso, siendo una fuente de incertidumbre la pureza del agua. Entre las impurezas están los gases disueltos, por lo que se requiere una desgasificación previa. La ecuación de estado de referencia más empleada para el agua es la de Span, R. et al. 2000. La temperatura afecta tanto al volumen del recipiente como a la densidad del patrón y la muestra. Con este sencillo diseño solo es posible medir a presión ambiente.
Distintos investigadores han propuesto modificaciones que permiten medir a presión con equipos más complejos.
3.2. Balanzas hidrostáticas.
Las balanzas hidrostáticas son uno de los métodos más sencillos para medir densidades. Su principio de medida está basado en el principio de Arquímedes, midiendo la fuerza del empuje ejercida sobre un cuerpo inmerso en el fluido. Dependiendo del rango de medida podemos encontrar diferentes tipos de balanzas.
El diseño más sencillo está formado por un flotador, que suele ser una esfera o un cilindro de cristal o metal, suspendido mediante un fino hilo de platino de una balanza comercial. La diferencia entre la masa verdadera del flotador y su masa aparente cuando está sumergido en el líquido dividida por el volumen del flotador nos da la densidad del líquido.
Es necesario determinar previamente el volumen del flotador, pudiendo realizar las correcciones a la medida debidas a la tensión superficial y al hilo de platino inmerso en el líquido.
Estas balanzas son muy útiles para medidas a presión ambiente y a en un rango moderado de temperaturas, pudiendo encontrar incertidumbres inferiores a ± 0,1 %.
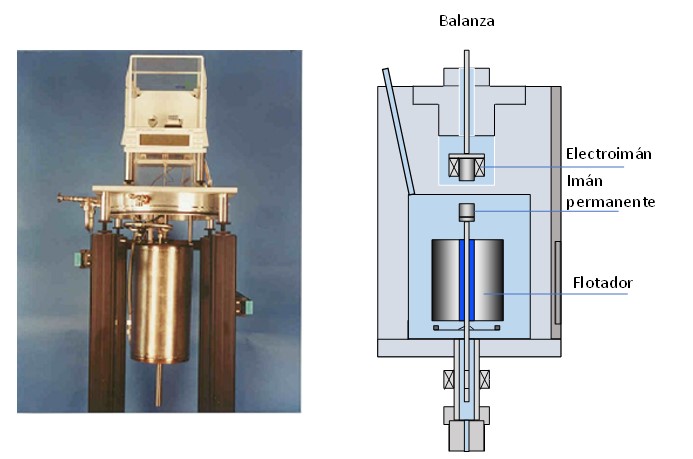
Las balanzas de flotador de suspensión magnética aplican el mismo principio de Arquímedes pero ahora el flotador está suspendido de la balanza mediante un acoplamiento magnético, lo que permite medir densidades de líquidos y gases a alta presión con bajas incertidumbres, inferiores a ± 0,02 %.
El flotador lleva acoplado un imán permanente y mediante un electroimán exterior el flotador se puede acoplar y desacoplar de la balanza. La densidad se determina dividiendo la diferencia de la masa del flotador en el vacío menos la masa del flotador en el fluido entre el volumen del flotador.
3.3. Densímetro de tubo vibrante.
Un densímetro de tubo vibrante consiste en un tubo de metal o cristal, de paredes delgadas, en forma de “U” o “V”, sujeto a una gran masa para aislar el tubo de perturbaciones mecánicas externas. Normalmente la longitud del tubo es de 5 cm a 10 cm, con un diámetro de 1,5 mm a 3 mm dependiendo de la presión. El tubo se llena con la muestra de ensayo y vibra perpendicularmente a su plano en un campo electromagnético; la frecuencia de la oscilación del tubo puede relacionarse directamente con la densidad del fluido contenido en el tubo.
En una de las posibles configuraciones la vibración se produce con un imán permanente adherido al tubo y una bobina. Una corriente alterna suministrada al circuito conductor produce oscilaciones estacionarias, las cuales inducen una señal eléctrica en el circuito de medida conectado al frecuencímetro.
La muestra se introduce en el interior del tubo donde se controla la presión y temperatura, existiendo equipos comerciales que alcanzan los 140 MPa para amplios rangos de temperaturas.
El tubo se comporta aproximadamente como un oscilador armónico simple, con lo que es posible relacionar el periodo con la masa del tubo y por tanto con la densidad del fluido contenido en el tubo.
\(2\pi\ f=\left(\frac{k}{M}\right)^{1/2}\)
Para obtener la densidad se realiza un calibrado con dos referencias. Uno de los métodos más estudiados emplea vacío y agua, obteniendo las constantes A y B de la ecuación
\(\rho(T,p)=A(T)({\ \tau}^2(T,p)-B(T,p)\)
El calibrado debe realizarse a cada presión y temperatura. La determinación de estas constantes constituye la principal fuente de incertidumbre, debido a las referencias y a la influencia de la presión y temperatura en la densidad. Se pueden conseguir incertidumbres inferiores a ± 0,05 %

3.4. Otros densímetros.
La densidad es una de las propiedades termofísicas más importantes (Wakeham et al.2007), por lo que existe un gran número de técnicas desarrolladas por los investigadores, en amplios rangos de temperatura y presión, para fluidos puros y mezclas, desde el estado de líquido comprimido, hasta fluido supercrítico, pasando por vapor y líquido saturados. Además de los densímetros descritos en este trabajo, podemos encontrar en la bibliografía densímetros de fuelle, densímetros isocóricos, densímetros de hilo vibrante, densímetros piezométricos, densímetro Burnett y densímetros relativos. Todos ellos tienen en común la necesidad de medir temperatura y presión junto a volumen y masa en densímetros primarios o patrones de densidad en densímetros secundarios.
4. CONCLUSIONES
La densidad es una propiedad termofísica esencial, tanto para el desarrollo de ecuaciones de estado, como para la investigación y la industria. En este trabajo nos hemos centrado en fluidos, líquidos y gases.
Históricamente se han desarrollado diferentes técnicas experimentales en función de las temperaturas, presiones y fase en la que se encentra la sustancia. La determinación de la variación de la densidad con la presión y temperatura es la base para el desarrollo de las ecuaciones de estado PυT. En este trabajo se han presentado tres técnicas, sin hacer un repaso exhaustivo de todas las técnicas sino de las más habituales. Describimos los más sencillos, picnómetros de líquidos; y los más exactos, balanzas de flotador de suspensión magnética; también exponemos los fundamentos de los más utilizados en la industria, densímetros de tubo vibrante.
BIBLIOGRAFÍA
Gupta and Olson. Industrial Needs in Physical Properties. Ind. Eng. Chem. Res. 2003, 42, 6359-6374.
Elliot, D. G.; Chen, J. J.; Brown, T. S.; Sloan, E. D.; Kidnay, A. J. The economic impact of fluid properties research on expander plants. Fluid Phase Equilibria 116 (1996) 27-38.
Experimental Thermodynamics Volume II. Experimental Thermodynamics of Non-reacting Fluids. Le Neindre, B.; Vodar, B., eds. For IUPAC, Butterworths, London, 1975.
Experimental Thermodynamics Volume VI. Measurement of the Thermodynamics Properties of Single Phases. Goodwin, A. R. H.; Marsh, K. N.; Wakeham, W. A., eds. For IUPAC, Elsevier Science, Amsterdam, 2002.
Span, R. Lemmon, E.W., Jacobsen, R.T, Wagner, W., and Yokozeki, A. “A Reference Equation of State for the Thermodynamic Properties of Nitrogen for Temperatures from 63.151 to 1000 K and Pressures to 2200 MPa,” J. Phys. Chem. Ref. Data, 29(6):1361-1433, 2000.
Wakeham, W. A.; Assael, M. A.; Atkinson, J. K.; Bilek, J.; Fareleira, J. M. N. A.; Fitt, A. D.; Goodwin, A. R. H.; Oliveira, C. M. B. P. Thermophysical property measurements: The journey from accuracy to fitness for purpose. Int. J. Thermophys. 2007, 28, 372-416.










Comentarios